
分析 (1)设男式单车x元/辆,女式单车y元/辆,根据“购买3辆男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元”列方程组求解可得;
(2)设购置女式单车m辆,则购置男式单车(m+4)辆,根据“两种单车至少需要22辆、购置两种单车的费用不超过50000元”列不等式组求解,得出m的范围,即可确定购置方案;再列出购置总费用关于m的函数解析式,利用一次函数性质结合m的范围可得其最值情况.
解答 解:(1)设男式单车x元/辆,女式单车y元/辆,
根据题意,得:$\left\{\begin{array}{l}{3x=4y}\\{5x+4y=16000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2000}\\{y=1500}\end{array}\right.$,
答:男式单车2000元/辆,女式单车1500元/辆;
(2)设购置女式单车m辆,则购置男式单车(m+4)辆,
根据题意,得:$\left\{\begin{array}{l}{m+m+4≥22}\\{2000(m+4)+1500m≤50000}\end{array}\right.$,
解得:9≤m≤12,
∵m为整数,
∴m的值可以是9、10、11、12,即该社区有四种购置方案;
设购置总费用为W,
则W=2000(m+4)+1500m=3500m+8000,
∵W随m的增大而增大,
∴当m=9时,W取得最小值,最小值为39500,
答:该社区共有4种购置方案,其中购置男式单车13辆、女式单车9辆时所需总费用最低,最低费用为39500元.
点评 本题主要考查二元一次方程组、一元一次不等式组及一次函数的应用,理解题意找到题目蕴含的相等关系或不等关系列出方程组或不等式组是解题的关键.


科目:初中数学 来源: 题型:解答题
| 用户每月用水量(m3) | 32及其以下 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43及其以上 |
| 户数(户) | 200 | 160 | 180 | 220 | 240 | 210 | 190 | 100 | 170 | 120 | 100 | 110 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=35}\\{2x+3y=90}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=35}\\{3x+2y=90}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=90}\\{2x+3y=35}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=90}\\{3x+2y=35}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
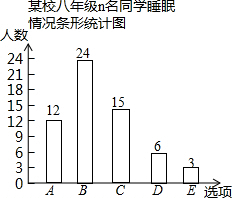 某校八年级学生会为了解本年级600名学生的睡眠情况,将同学们某天的睡眠时长t(小时)分为A,B,C,D,E(A:9≤t≤24;B:8≤t<9;C:7≤t<8;D:6≤t<7;E:0≤t<6)五个选项,进行了一次问卷调查,随机抽取n名同学的调查问卷并进行了整理,绘制成如下条形统计图,根据统计图提供的信息解答下列问题:
某校八年级学生会为了解本年级600名学生的睡眠情况,将同学们某天的睡眠时长t(小时)分为A,B,C,D,E(A:9≤t≤24;B:8≤t<9;C:7≤t<8;D:6≤t<7;E:0≤t<6)五个选项,进行了一次问卷调查,随机抽取n名同学的调查问卷并进行了整理,绘制成如下条形统计图,根据统计图提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
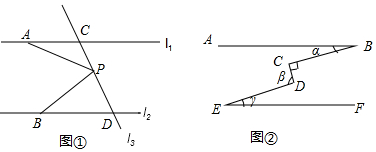
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.45×1010 | B. | 0.145×109 | C. | 1.45×108 | D. | 14.5×108 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com