
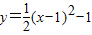 向右平移2个单位,再向上平移2个单位所得抛物线的解析式为 .
向右平移2个单位,再向上平移2个单位所得抛物线的解析式为 .  (x-h)2+k,把新抛物线的顶点坐标代入即可求解.抛物线的平移不改变二次项的系数.
(x-h)2+k,把新抛物线的顶点坐标代入即可求解.抛物线的平移不改变二次项的系数. (x-h)2+k,
(x-h)2+k, (x-3)2+1.
(x-3)2+1.

科目:初中数学 来源: 题型:
| 3 |
| 4 |
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:关于![]() 的一元二次方程
的一元二次方程![]() (m为实数)
(m为实数)
1.若方程有两个不相等的实数根,求![]() 的取值范围;
的取值范围;
2.在(1)的条件下,求证:无论![]() 取何值,抛物线
取何值,抛物线![]() 总过
总过![]() 轴上的一个固定点;
轴上的一个固定点;
3.若![]() 是整数,且关于
是整数,且关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的整数根,把抛物线
有两个不相等的整数根,把抛物线![]() 向右平移3个单位长度,求平移后的解析式.
向右平移3个单位长度,求平移后的解析式.
查看答案和解析>>
科目:初中数学 来源:2012届北京海淀区中考模拟数学卷 题型:解答题
已知:关于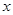 的一元二次方程
的一元二次方程 (m为实数)
(m为实数)
【小题1】若方程有两个不相等的实数根,求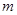 的取值范围;
的取值范围;
【小题2】在(1)的条件下,求证:无论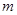 取何值,抛物线
取何值,抛物线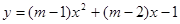 总过
总过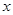 轴上的一个固定点;
轴上的一个固定点;
【小题3】若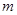 是整数,且关于
是整数,且关于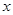 的一元二次方程
的一元二次方程 有两个不相等的整数根,把抛物线
有两个不相等的整数根,把抛物线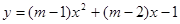 向右平移3个单位长度,求平移后的解析式.
向右平移3个单位长度,求平移后的解析式.
查看答案和解析>>
科目:初中数学 来源:2010-2011学年新人教版九年级(上)第三次月考数学试卷(26-27章)(解析版) 题型:填空题
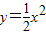 向右平移2个单位,再向上平移1个单位,所的抛物线的解析式为 .
向右平移2个单位,再向上平移1个单位,所的抛物线的解析式为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com