
【题目】如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
(1)求∠DCE的度数;
(2)若AB=4,CD=3AD,求DE的长.

【答案】(1)90°(2)2![]()
【解析】试题分析:(1)首先由等腰直角三角形的性质求得∠BAD、∠BCD的度数,然后由旋转的性质可求得∠BCE的度数,故此可求得∠DCE的度数;
(2)由(1)可知△DCE是直角三角形,先由勾股定理求得AC的长,然后依据比例关系可得到CE和DC的长,最后依据勾股定理求解即可.
试题解析:(1)∵△ABCD为等腰直角三角形,
∴∠BAD=∠BCD=45°.
由旋转的性质可知∠BAD=∠BCE=45°.
∴∠DCE=∠BCE+∠BCA=45°+45°=90°.
(2)∵BA=BC,∠ABC=90°,
∴AC=![]() .
.
∵CD=3AD,
∴AD=![]() ,DC=3
,DC=3![]() .
.
由旋转的性质可知:AD=EC=![]() .
.
∴DE=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知点(﹣2,y1),(﹣4,y,2)在函数y=x2﹣4x+7的图象上,那么y1 , y2的大小关系是( )
A.y1>y2
B.y1=y2
C.y1<y2
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
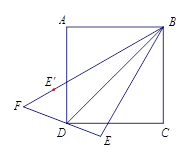
【题目】如图,四边形 ![]() 是正方形,
是正方形, ![]() 是
是 ![]() 垂直平分线上的点,点
垂直平分线上的点,点 ![]() 关于
关于 ![]() 的对称点是
的对称点是 ![]() ,直线
,直线 ![]() 与直线
与直线 ![]() 交于点
交于点 ![]() .
.
(1)若点 ![]() 是
是 ![]() 边的中点,连接
边的中点,连接 ![]() ,则
,则 ![]() =;
=;
(2)小明从老师那里了解到,只要点 ![]() 不在正方形的中心,则直线
不在正方形的中心,则直线 ![]() 与
与 ![]() 所夹锐角不变.他尝试改变点
所夹锐角不变.他尝试改变点 ![]() 的位置,计算相应角度,验证老师的说法.
的位置,计算相应角度,验证老师的说法.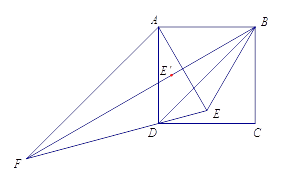
如图,将点 ![]() 选在正方形内,且△
选在正方形内,且△ ![]() 为等边三角形,求出直线
为等边三角形,求出直线 ![]() 与
与 ![]() 所夹锐角的度数;
所夹锐角的度数;
(3)请你继续研究这个问题,可以延续小明的想法,也可用其它方法.
我选择小明的想法;并简述求直线 ![]() 与
与 ![]() 所夹锐角度数的思路.
所夹锐角度数的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB =90°,∠ABC=30°,将△ABC绕点C顺时针旋转 ![]() 角(0°<
角(0°< ![]() <180°)至△A′B′C , 使得点A′恰好落在AB边上,则
<180°)至△A′B′C , 使得点A′恰好落在AB边上,则 ![]() 等于( ).
等于( ).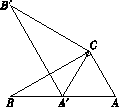
A.150°
B.90°
C.60°
D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,动点A(a,0)在x轴的正半轴上,定点B(m, n)在第一象限内(m<2≤a).在△OAB外作正方形ABCD和正方形OBEF , 连接FD , 点M为线段FD的中点.作BB1⊥x轴于点B1 , 作FF1⊥x轴于点F1.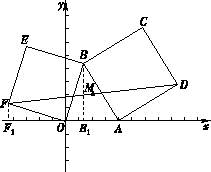
(1)填空:由△≌△ , 及B(m, n)可得点F的坐标为 , 同理可得点D的坐标为;(说明:点F , 点D的坐标用含m , n , a的式子表示)
(2)直接利用(1)的结论解决下列问题:
①当点A在x轴的正半轴上指定范围内运动时,点M总落在一个函数图象上,求该函数的解析式(不必写出自变量x的取值范围);
②当点A在x轴的正半轴上运动且满足2≤a≤8时,求点M所经过的路径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短.横之不出四尺,纵之不出二尺,斜之适出注.问户斜几何.
注释:横放,竿比门宽长出四尺;竖放,竿比门高长出二尺;斜放恰 好能出去.解决下列问题: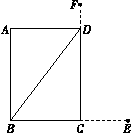
(1)示意图中,线段CE的长为尺,线段DF的长为尺;
(2)求户斜多长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a、b、c为平面上三条不同直线,
(1)若a∥b,b∥c,则a与c的位置关系是________;
(2)若a⊥b,b⊥c,则a与c的位置关系是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( ) 
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com