练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：如图，∠1=∠2．求证：∠3 +∠4=180°．

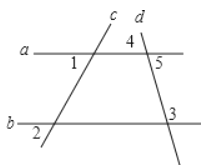
    证明：∵∠1=∠2（已知）

    ∴ a∥b（ 　 　 ）

    ∴∠3 +∠5=180° （两直线平行，同旁内角互补）

    又 ∵∠4=∠5 （ 　 　 ）

    ∴∠3 +∠4=180° （等量代换）

    【答案】同位角相等,两直线平行;两直线平行,同旁内角互补;对顶角相等．

    【解析】

    先判定a∥b,即可得出∠3+∠5=180°,再根据对顶角相等,即可得到∠4=∠5,进而得出∠3+∠4 =180°．

    证明:∵∠1=∠2,

    ∴a∥b （同位角相等,两直线平行）,

    ∴∠3+∠5=180° （两直线平行，同旁内角互补）,

    又∵∠4=∠5（对顶角相等）,

    ∴∠3+∠4=180°.

    故答案为:同位角相等,两直线平行;两直线平行,同旁内角互补;对顶角相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知Rt△ABC中，∠B=90°，∠A=60°，AC=2+4，点M、N分别在线段AC、AB上，将△ANM沿直线MN折叠，使点A的对应点D恰好落在线段BC上，当△DCM为直角三角形时，折痕MN的长为__．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有四张相同的卡片，分别写有数字2，0，1，5，将它们背面朝上（背面无差别）洗匀后放在桌上．

    （1）从中任意抽出一张，抽到卡片上的数字为负数的概率；

    （2）从中任意抽出两张，用树状图或表格列出所有可能的结果，并求抽出卡片上的数字积为正数的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

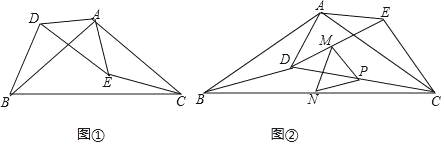
    【题目】如图①，在等腰△ABC和△ADE中，AB=AC，AD=AE，且∠BAC=∠DAE=120°．

    （1）求证：△ABD≌△ACE；

    （2）把△ADE绕点A逆时针方向旋转到图②的位置，连接CD，点M、P、N分别为DE、DC、BC的中点，连接MN、PN、PM，判断△PMN的形状，并说明理由；

    （3）在（2）中，把△ADE绕点A在平面内自由旋转，若AD=4，AB=6，请分别求出△PMN周长的最小值与最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD中，已知AB=3，点E，F分别在BC、CD上，且∠BAE=30°，∠DAF=15°，则△AEF的面积为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，一次函数y=kx+b的图象与反比例函数y=的图象相交于点A（m，3）、B（﹣6，n），与x轴交于点C．

    （1）求一次函数y=kx+b的关系式；

    （2）结合图象，直接写出满足kx+b＞的x的取值范围；

    （3）若点P在x轴上，且S△ACP=S△BOC，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C=90°，以AC为直径作⊙O，交AB于D，过点O作OE∥AB，交BC于E．

    （1）求证：ED为⊙O的切线；

    （2）如果⊙O的半径为，ED=2，延长EO交⊙O于F，连接DF、AF，求△ADF的面积．

    【答案】（1）证明见解析；（2）

    【解析】试题分析：（1）首先连接OD，由OE∥AB，根据平行线与等腰三角形的性质，易证得≌ 即可得，则可证得为的切线；
    （2）连接CD，根据直径所对的圆周角是直角，即可得 利用勾股定理即可求得的长，又由OE∥AB，证得根据相似三角形的对应边成比例，即可求得的长，然后利用三角函数的知识，求得与的长，然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案．

    试题解析：(1)证明：连接OD，

    ∵OE∥AB，

    ∴∠COE=∠CAD，∠EOD=∠ODA，

    ∵OA=OD,

    ∴∠OAD=∠ODA，

    ∴∠COE=∠DOE，

    在△COE和△DOE中，

    ∴△COE≌△DOE(SAS)，

    ∴ED⊥OD，

    ∴ED是的切线；

    (2)连接CD，交OE于M，

    在Rt△ODE中，

    ∵OD=32，DE=2，

    ∵OE∥AB，

    ∴△COE∽△CAB，

    ∴AB=5，

    ∵AC是直径，

    ∵EF∥AB，

    ∴S△ADF=S梯形ABEFS梯形DBEF

    ∴△ADF的面积为

    【题型】解答题
    【结束】
    25

    【题目】【题目】已知，抛物线y=ax2+ax+b（a≠0）与直线y=2x+m有一个公共点M（1，0），且a＜b．

    （1）求b与a的关系式和抛物线的顶点D坐标（用a的代数式表示）；

    （2）直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；

    （3）a=﹣1时，直线y=﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位（t＞0），若线段GH与抛物线有两个不同的公共点，试求t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

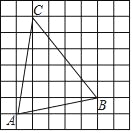
    【题目】在每个小正方形的边长为1的网格中，点A、B、C均在格点上，在△ABC的内部有一点P，满足S△PAB：S△PBC：S△PCA=1：2：3，请在如图所示的网格中，用无刻度直尺画出点P（保留画图痕迹）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

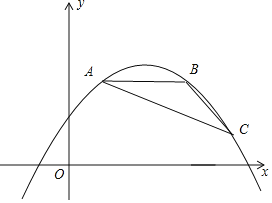
    【题目】如图，点A，B，C都在抛物线y=ax2﹣2amx+am2+2m﹣5（其中﹣＜a＜0）上，AB∥x轴，∠ABC=135°，且AB=4．

    （1）填空：抛物线的顶点坐标为 （用含m的代数式表示）；

    （2）求△ABC的面积（用含a的代数式表示）；

    （3）若△ABC的面积为2，当2m﹣5≤x≤2m﹣2时，y的最大值为2，求m的值．

    查看答案和解析>>

    同步练习册答案