
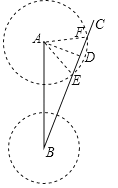
【题目】如图,气象部门观测到距A市正南方向240km的B处有一台风中心,其中心最大风力为12级,该台风中心正以20km/h的速度沿北偏东30°的BC方向移动,且台风中心风力不变,已知每远离台风中心20km,风力就减弱一级,台风中心在移动的过程中,其周围130km的范围内都要受到影响.
(1)A市是否会受到这次台风影响?若受台风影响,则所受的最大风力是几级?
(2)A市遭受到这次台风影响多长时间?

【答案】(1)A市会受到这次台风影响,6(级);(2)5小时.
【解析】
(1)求是否会受到台风的影响,其实就是求A到BC的距离是否大于台风影响范围的半径,如果大于,则不受影响,反之则受影响.如果过A作AD⊥BC于D,AD就是所求的线段.直角三角形ABD中,由∠ABD的度数和AB的长,AD就不难求出了.风力最大时,台风中心应该位于D点,然后根据题目给出的条件判断出是几级风.
(2)受台风影响时,台风中心移动的距离,应该是A为圆心,台风影响范围的半径为半径,所得圆截得的BC上的线段的长即EF得长,可通过在直角三角形AED和AFD中,根据勾股定理求得.有了路程,有了速度,时间就可以求出了.
(1)A市会受到这次台风的影响.理由如下:
过A作AD⊥BC于点D.
∵在直角△ABD中,∠B=30°,∴AD=![]() AB=
AB=![]() ×240=120km<130 km,则A市受到这次台风影响.
×240=120km<130 km,则A市受到这次台风影响.
12-120÷20=12-6=6(级).
(2)如图以A为圆心,130为半径作⊙A交BC于E、F,则AE=AF=130,∴台风影响该市持续的路程为:EF=2DE=2![]() 100(km),∴台风影响该市的持续时间t=100÷20=5(小时).
100(km),∴台风影响该市的持续时间t=100÷20=5(小时).


科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角板ABC的斜边AB与量角器的直径重合,点D是量角器上60°刻度线的外端点,连接CD交AB于点E,则∠CEB的度数为( )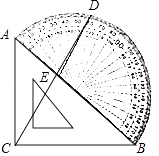
A.60°
B.65°
C.70°
D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+ ![]() 经过A(1,0),B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边三角形ABC.
经过A(1,0),B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边三角形ABC.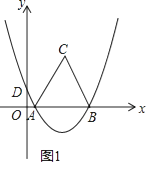
(1)求抛物线的解析式;
(2)在x轴上方的抛物线上是否存在点M,是S△ABM= ![]() S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)如图2,E是线段AC上的动点,F是线段BC上的动点,AF与BE相交于点P.
①若CE=BF,试猜想AF与BE的数量关系及∠APB的度数,并说明理由;
②若AF=BE,当点E由A运动到C时,请直接写出点P经过的路径长.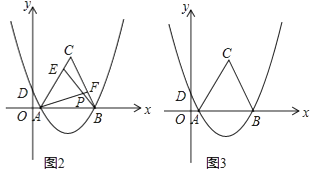
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了搞好对“传统文化学习”的宣传活动,对本校部分学生(随机抽查)进行了一次相关知识了解程度的调查测试(成绩分为A、B、C、D、E五个组,x表示测试成绩).通过对测试成绩的分析,得到如图所示的两幅不完整的统计图.请你根据图中提供的信息解答以下问题: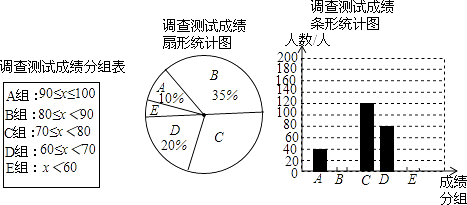
(1)参加调查测试的学生为人;
(2)将条形统计图补充完整;
(3)本次调查测试成绩中的中位数落在组内;
(4)若测试成绩在80分以上(含80分)为优秀,该中学共有学生2600人,请你根据样本数据估计全校学生测试成绩为优秀的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点,PA=3,PB=1,CD=PC=2,CD⊥PC.
(1)找出图中一对全等三角形,并证明;
(2)求∠BPC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
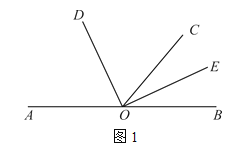
【题目】已知,O为直线AB上一点,∠DOE=90°.
(1)如图1,若∠AOC=130°,OD平分∠AOC.
①求∠BOD的度数;
②请通过计算说明OE是否平分∠BOC.
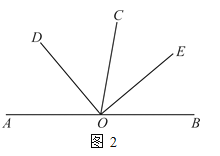
(2)如图2,若∠BOE:∠AOE=2:7,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是线段AB上一点,AB=12cm,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上),运动的时间为t.
![]()
(1)当t=1时,PD=2AC,请求出AP的长;
(2)当t=2时,PD=2AC,请求出AP的长;
(3)若C、D运动到任一时刻时,总有PD=2AC,请求出AP的长;
(4)在(3)的条件下,Q是直线AB上一点,且AQ﹣BQ=PQ,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B,C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为 . 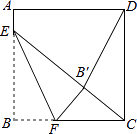
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为BC边上一点,连结AE.已知AB=8,CE=2,F是线段AE上一动点.若BF的延长线交正方形ABCD的一边于点G,且满足AE=BG,则 ![]() 的值为 .
的值为 . 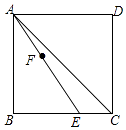
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com