
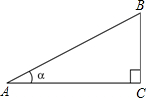
 ��ͼ�����壺��ֱ��������ABC�У���Ǧ����ڱ���ԱߵıȽ����Ǧ������У�����ctan������ctan��=$\frac{�Ǧ����ڱ�}{�Ǧ��ĶԱ�}$=$\frac{AC}{BC}$�����������ǵ����ж��壬���������⣺
��ͼ�����壺��ֱ��������ABC�У���Ǧ����ڱ���ԱߵıȽ����Ǧ������У�����ctan������ctan��=$\frac{�Ǧ����ڱ�}{�Ǧ��ĶԱ�}$=$\frac{AC}{BC}$�����������ǵ����ж��壬���������⣺���� ��1������=30��ʱ������������ֵ�����$\frac{BC}{AC}$��ֵ���������еĶ������ô𰸣�
��2�������к����Ķ����֪$\frac{BC}{AC}$��ֵ��������$\frac{AC}{BC}$��ֵ�������ctanA��ֵ��
��3������A��B�ֱ���x��Ĵ��ߣ�����ֱ�ΪC��D�����֤�á�OAC�ס�BOD����ctanA=$\frac{\sqrt{3}}{3}$������������Ʊȣ������á�BOD�������������k��ֵ��
��� �⣺
��1����tan��=$\frac{BC}{AC}$��
��tan30��=$\frac{BC}{AC}$=$\frac{\sqrt{3}}{3}$��
��$\frac{AC}{BC}$=$\sqrt{3}$��
��ctan30��=$\frac{AC}{BC}$=$\sqrt{3}$��
�ʴ�Ϊ��$\sqrt{3}$��
��2����Rt��ABC��tanA=$\frac{BC}{AC}$=$\frac{3}{4}$��
��$\frac{AC}{BC}$=$\frac{4}{3}$��
��ctanA=$\frac{4}{3}$��
��3����ͼ���ֱ����A��B��x��Ĵ��ߣ�����ֱ�ΪC��D��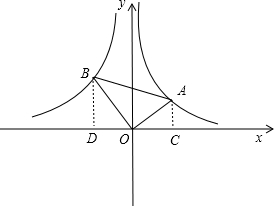
��A�ڷ���������y=$\frac{2}{x}$��ͼ���ϣ�
��S��AOC=$\frac{1}{2}$OC•AC=$\frac{1}{2}$��2=1��
��ctanA=$\frac{\sqrt{3}}{3}$��
��$\frac{OA}{OB}$=$\frac{\sqrt{3}}{3}$��
��OA��OB��
���AOC+��BOD=��BOD+��OBD=90�㣬
���AOC=��OBD���ҡ�ACO=��BDO=90�㣬
���OAC�ס�BOD��
��$\frac{{S}_{��OAC}}{{S}_{��BOD}}$=��$\frac{OA}{OB}$��2=��$\frac{\sqrt{3}}{3}$��2=$\frac{1}{3}$����$\frac{1}{{S}_{��BOD}}$=$\frac{1}{3}$��
��S��BOD=3��
��S��BOD=$\frac{1}{2}$OD•BD=-$\frac{1}{2}$k��
��-$\frac{1}{2}$k=3�����k=-6��
���� ����Ϊ�������������ۺ�Ӧ�ã��漰���Ǻ����Ķ��塢�ر�ǵ����Ǻ���ֵ�����������ε��ж������ʡ�������������k�ļ��������֪ʶ���ڣ�1������2������������ֵ�Ķ����ǽ���Ĺؼ����ڣ�3������á�BOD������ǽ���Ĺؼ�������Ϊ�¶�������Ŀ���ؼ���������Ŀ���������¶��壬�ѶȲ���


 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
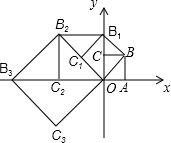 ��ͼ����ƽ��ֱ������ϵ����һ�߳�Ϊ1��������OABC����OA��OC�ֱ���x�ᡢy���ϣ�����ԶԽ���OBΪ�����ڶ���������OBB1C1�����ԶԽ���OB1Ϊ����������������OB1B2C2���մ˹�������ȥ�����B2015������Ϊ��������
��ͼ����ƽ��ֱ������ϵ����һ�߳�Ϊ1��������OABC����OA��OC�ֱ���x�ᡢy���ϣ�����ԶԽ���OBΪ�����ڶ���������OBB1C1�����ԶԽ���OB1Ϊ����������������OB1B2C2���մ˹�������ȥ�����B2015������Ϊ��������| A�� | ��21008��0�� | B�� | ��21007��-21007�� | C�� | ��21009��21009�� | D�� | ��-21007��21007�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ֱ������ϵ�У���A�Ƿ���������y1=$\frac{k}{x}$ͼ����һ�㣬AB��x����������ڵ�B����C��OB���е㣬һ�κ���y2=ax+b��ͼ��A��C���㣬��y���ڵ�D��0��-2������AOB�����Ϊ4
��ͼ����ֱ������ϵ�У���A�Ƿ���������y1=$\frac{k}{x}$ͼ����һ�㣬AB��x����������ڵ�B����C��OB���е㣬һ�κ���y2=ax+b��ͼ��A��C���㣬��y���ڵ�D��0��-2������AOB�����Ϊ4�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
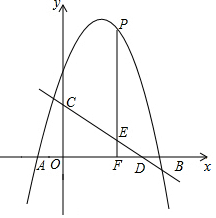 ��ͼ��������y=-x2+4x+5��x�ύ��A��B���㣨��A�ڵ�B����ࣩ��ֱ��y=$-\frac{3}{4}x+3$��y�ύ�ڵ�C����x�ύ�ڵ�D��P��x���Ϸ�����������һ���㣬����P��PF��x���ڵ�F����ֱ��CD�ڵ�E�����P�ĺ�����Ϊm��
��ͼ��������y=-x2+4x+5��x�ύ��A��B���㣨��A�ڵ�B����ࣩ��ֱ��y=$-\frac{3}{4}x+3$��y�ύ�ڵ�C����x�ύ�ڵ�D��P��x���Ϸ�����������һ���㣬����P��PF��x���ڵ�F����ֱ��CD�ڵ�E�����P�ĺ�����Ϊm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com