
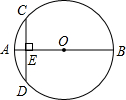
 (2012•朝阳)如图,AB为⊙O的直径,CD为⊙O的一条弦,CD⊥AB,垂足为E,已知CD=6,AE=1,则⊙0的半径为
(2012•朝阳)如图,AB为⊙O的直径,CD为⊙O的一条弦,CD⊥AB,垂足为E,已知CD=6,AE=1,则⊙0的半径为科目:初中数学 来源: 题型:
 (2012•朝阳)如图所示中的折线ABC为甲地向乙地打长途电话需付的电话费y(元)与通话时间t(分钟)之间的函数关系,则通话8分钟应付电话费
(2012•朝阳)如图所示中的折线ABC为甲地向乙地打长途电话需付的电话费y(元)与通话时间t(分钟)之间的函数关系,则通话8分钟应付电话费查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•朝阳)如图已知P为⊙O外一点,PA为⊙O的切线,B为⊙O上一点,且PA=PB,C为优弧
(2012•朝阳)如图已知P为⊙O外一点,PA为⊙O的切线,B为⊙O上一点,且PA=PB,C为优弧 |
| AB |
| 2 |
| 3 |
| 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•朝阳)如图,△ABC三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点C顺时针旋转到△A′B′C的位置,且A′、B′仍落在格点上,则线段AC扫过的扇形所围成的圆锥体的底面半径是
(2012•朝阳)如图,△ABC三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点C顺时针旋转到△A′B′C的位置,且A′、B′仍落在格点上,则线段AC扫过的扇形所围成的圆锥体的底面半径是
| ||
| 4 |
| ||
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
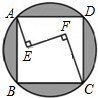 (2012•朝阳)如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=4,EF=8,FC=12,则正方形与其外接圆形成的阴影部分的面积为
(2012•朝阳)如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=4,EF=8,FC=12,则正方形与其外接圆形成的阴影部分的面积为查看答案和解析>>
科目:初中数学 来源: 题型:
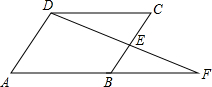 (2012•朝阳)如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于F点,AB=BF,请你添加一个条件(不需再添加任何线段或字母),使之能推出四边形ABCD为平行四边形,请证明.你添加的条件是
(2012•朝阳)如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于F点,AB=BF,请你添加一个条件(不需再添加任何线段或字母),使之能推出四边形ABCD为平行四边形,请证明.你添加的条件是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com