
����Ŀ��ij�С�ÿ�����һСʱ���Ҹ�����һ���ӡ���ѿ�չ��һ�꣬Ϊ�˽���д����Ŀ�չ�����ij����ͳ�ƹ�˾���������µ��鷽ʽ�е�һ�ֽ��е��飺
A����һ���������ѡȡ200������
B����һ������IJ�ͬסլ¥�����ѡȡ200������
C���Ӹ��й����ֻ��������������ȡ200�����������Ϊ�������Ȼ����е��飮
(1)���������鷽ʽ�У�����Ϊ�ȽϺ�����һ����________(�����)��
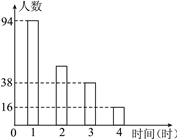
(2)��һ�ֱȽϺ����ĵ��鷽ʽ���õ��������Ƴ�����ͼ��ʾ������ͳ��ͼ������������У���200������ÿ�����2Сʱ��������________�ˣ�
(3)��������100���ˣ���������(2)�еĵ����������Ƹ���ÿ�����2Сʱ�����ϵ������Ƕ��٣�
(4)��������100���ˣ�����Ϊ��������������û�в������ĵط���̸̸������ɣ�
���𰸡�(1)C��(2)52��(3)���Ƹ���ÿ�����2Сʱ�����ϵ�������53���ˣ�(4)�У����ɼ�����.
��������
��1�����������Ƿ���д����Խ�ɣ�
��2����200��ȥ����3������˻����ɣ�
��3�������200����ÿ�����2Сʱ�����ϵ��������ټ���100������ÿ�����2Сʱ�����ϵ�������
��4��ֻҪ�����⼴�ɣ�
(1) A��B���ֵ��鷽ʽ����Ƭ���ԣ���C�ȽϺ�������
(2)200-94-38-16=52��
(3) ![]() ��100��53(����)��
��100��53(����)��
�ʹ��Ƹ���ÿ�����2Сʱ�����ϵ�������53���ˣ�
(4)�У�����ȫ����100���ˣ�������ֻѡȡ��200�ˣ�����������С������ȷ�ر������ʵ�����(�𰸲�Ψһ����������).



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��ax2��2ax+c(a��0)��ͼ�����A(3��m)��
(1)��a����1��m��0ʱ���������ߵĶ�������_____��
(2)��ͼ��ֱ��l��y��kx+c(k��0)����������B��C���㣬��Q(x��y)���������ϵ�B��C֮���һ�����㣬��QD��x�ύֱ��l�ڵ�D����QE��y���ڵ�E������DE�����QED��������2��x��4ʱ����ǡ������30�������60�㣬a��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
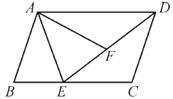
����Ŀ����ͼ����ƽ���ı���ABCD�У���B=��AFE��EA�ǡ�BEF��ƽ���ߣ���֤��
(1)��ABE�ա�AFE��
(2)��FAD=��CDE.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�Ա�У����ѧ����ɼ�ͥ��ҵ��ʱ�������������ƣ��涨ѧ��ÿ����ɼ�ͥ��ҵ��ʱ������1.5Сʱ����У��ѧ������ȤС��Ա�У����ѧ���ؼ������ҵ��ʱ������һ������������飬�����Ƴ�Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��һ���֣�
ʱ��(ʱ) | Ƶ�� | Ƶ�� |
0��t��0.5 | 4 | 0.1 |
0.5��t��1 | a | 0.3 |
1��t��1.5 | 10 | 0.25 |
1.5��t��2 | 8 | b |
2��t��2.5 | 6 | 0.15 |
�ϼ� | 1 |
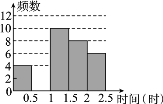
(1)��Ƶ���ֲ����У�a��________��b��________��
(2)��ȫƵ���ֲ�ֱ��ͼ��
(3)����Ƹ�У1400������ѧ���У��ж�����ѧ����1.5Сʱ����(������1.5Сʱ)����˼�ͥ��ҵ��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
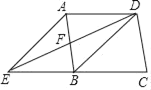
����Ŀ����ͼ����ƽ���ı���ABCD�У�DB��DA����ADB�Ľ�ƽ������AB�ཻ�ڵ�F����CB���ӳ����ཻ�ڵ�E����AE��
��1����֤���ı���AEBD�����Σ�
��2�����ı���ABCD�����Σ�DC��10��������AEBD��������� ������ֱ����գ�����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��![]() x+2��x�ύ�ڵ�A����y�ύ�ڵ�B��������y����
x+2��x�ύ�ڵ�A����y�ύ�ڵ�B��������y����![]() x2+bx+c����A��B���㣬��x�����һ������Ϊ C��
x2+bx+c����A��B���㣬��x�����һ������Ϊ C��
��1���������ߵĽ���ʽ��
��2������ͼ��ֱ��д������![]() x+2�ݩ�
x+2�ݩ�![]() x2+bx+c��x��ȡֵ��Χ��
x2+bx+c��x��ȡֵ��Χ��
��3�����DΪ���������ϵ�һ�㡢����AD������DAC����CBO�����D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() �뷴��������
�뷴��������![]() ��ͼ����A��1��4����B��4��n�����㣮
��ͼ����A��1��4����B��4��n�����㣮

��1������������һ�κ����Ľ���ʽ��
��2��ֱ��д����x��0ʱ��![]() �Ľ⼯��
�Ľ⼯��
��3����P��x���ϵ�һ���㣬��ȷ����P������������꣬ʹPA+PB��С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���ʵؾ��ȵ����������ӵ��������Ϸֱ����1��6�ĵ���.�������������Σ�����һ�Σ�������һ��ĵ�����Ϊ![]() �����ڶ��Σ�������һ��ĵ�����Ϊ
�����ڶ��Σ�������һ��ĵ�����Ϊ![]() ����㣨
����㣨![]() ������ֱ��
������ֱ��![]() �ϵĸ���Ϊ��
�ϵĸ���Ϊ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�У�AB=8����P�ڱ�CD�ϣ�tan��PBC=![]() ����Q��������BP�ϵ�һ�����㣬����Q��AB��ƽ���߽�����AD�ڵ�M����R������AD�ϣ�ʹRQʼ����ֱ��BP��ֱ��
����Q��������BP�ϵ�һ�����㣬����Q��AB��ƽ���߽�����AD�ڵ�M����R������AD�ϣ�ʹRQʼ����ֱ��BP��ֱ��
��1����ͼ1������R���D�غ�ʱ����PQ�ij���
��2����ͼ2����̽���� ![]() �ı�ֵ�Ƿ����Q���˶��������仯�����б仯����˵��������ɣ���û�б仯����������ı�ֵ��
�ı�ֵ�Ƿ����Q���˶��������仯�����б仯����˵��������ɣ���û�б仯����������ı�ֵ��
��3����ͼ3������Q���߶�BP�ϣ���PQ=x��RM=y����y����x�ĺ�����ϵʽ����д�����Ķ�����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com