
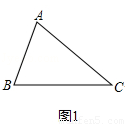
(1)如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形,并证明:BE=CD;(尺规作图,不写做法,保留作图痕迹);
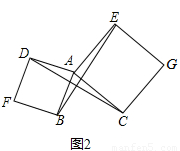
(2)如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE与CD有什么数量关系?简单说明理由;
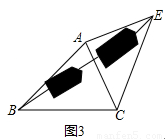
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:
如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.
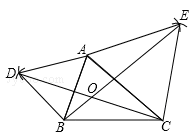
(1)如图所示:
(2)BE=CD
(3) 米
米
【解析】
分析:(1)分别以A、B为圆心,AB长为半径画弧,两弧交于点D,连接AD,BD,同理连接AE,CE,如图所示,由三角形ABD与三角形ACE都是等边三角形,得到三对边相等,两个角相等,都为60度,利用等式的性质得到夹角相等,利用SAS得到三角形ABD与三角形ACE全等,利用全等三角形的对应边相等即可得证。
(2)BE=CD,理由与(1)同理。
(3)根据(1)、(2)的经验,过A作等腰直角三角形ABD,连接CD,由AB=AD=100,利用勾股定理求出BD的长,由题意得到三角形DBC为直角三角形,利用勾股定理求出CD的长,即为BE的长。
解:(1)完成图形,如图所示:

证明:∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°。
∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB。
∵在△CAD和△EAB中, ,
,
∴△CAD≌△EAB(SAS)。∴BE=CD。
(2)BE=CD,理由同(1):
∵四边形ABFD和ACGE均为正方形,
∴AD=AB,AC=AE,∠BAD=∠CAE=90°。∴∠CAD=∠EAB。
∵在△CAD和△EAB中, ,
,
∴△CAD≌△EAB(SAS)。∴BE=CD;。
(3)由(1)、(2)的解题经验可知,过A作等腰直角三角形ABD,∠BAD=90°,
则AD=AB=100米,∠ABD=45°,∴BD=100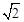 米。
米。
连接CD,则由(2)可得BE=CD。
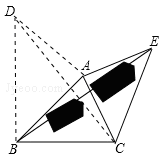
∵∠ABC=45°,∴∠DBC=90°。
在Rt△DBC中,BC=100米,BD=100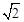 米,
米,
根据勾股定理得: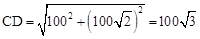 (米)。
(米)。
∴BE=CD=  米。
米。


科目:初中数学 来源: 题型:
 下列说法:
下列说法:| 2 |
| x |
| k |
| x |
| A、0 | B、1 | C、2 | D、5 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
| k |
| x |

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com