
【题目】已知如图 1,在△ABC 中,∠ACB=90°,BC=AC,点 D 在 AB 上,DE⊥AB交 BC 于 E,点 F 是 AE 的中点
(1) 写出线段 FD 与线段 FC 的关系并证明;
(2) 如图 2,将△BDE 绕点 B 逆时针旋转α(0°<α<90°),其它条件不变,线段 FD 与线段 FC 的关系是否变化,写出你的结论并证明;
(3) 将△BDE 绕点 B 逆时针旋转一周,如果 BC=4,BE=2![]() ,直接写出线段 BF 的范围.
,直接写出线段 BF 的范围.

【答案】(1)结论:FD=FC,DF⊥CF;(2)结论不变.(3)![]() ≤BF≤3
≤BF≤3![]() .
.
【解析】
(1)根据直角三角形的性质先找出相关角、边的关系,利用等量代换得到结果.(2)旋转前后,图形的性质是不变的,据此可以直接找到旋转前后边角的关系,从而证明结论(3)要使BF最长,只有点E落在AB上即可要使BF最短,只有点E落在AB的延长线即可.
(1)结论:FD=FC,DF⊥CF.
理由:如图1中,
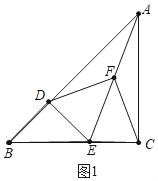
∵∠ADE=∠ACE=90°,AF=FE,
∴DF=AF=EF=CF,
∴∠FAD=∠FDA,∠FAC=∠FCA,
∴∠DFE=∠FDA+∠FAD=2∠FAD,∠EFC=∠FAC+∠FCA=2∠FAC,
∵CA=CB,∠ACB=90°,
∴∠BAC=45°,
∴∠DFC=∠EFD+∠EFC=2(∠FAD+∠FAC)=90°,
∴DF=FC,DF⊥FC.
(2)结论不变.
理由:如图2中,延长AC到M使得CM=CA,延长ED到N,使得DN=DE,连接BN、BM.EM、AN,延长ME交AN于H,交AB于O.
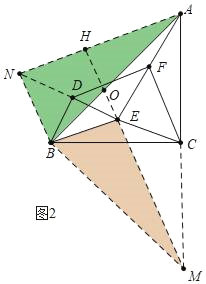
∵BC⊥AM,AC=CM,
∴BA=BM,同法BE=BN,
∵∠ABM=∠EBN=90°,
∴∠NBA=∠EBM,
∴△ABN≌△MBE,
∴AN=EM,∴∠BAN=∠BME,
∵AF=FE,AC=CM,
∴CF=![]() EM,FC∥EM,同法FD=
EM,FC∥EM,同法FD=![]() AN,FD∥AN,
AN,FD∥AN,
∴FD=FC,
∵∠BME+∠BOM=90°,∠BOM=∠AOH,
∴∠BAN+∠AOH=90°,
∴∠AHO=90°,
∴AN⊥MH,FD⊥FC.
(3)如图3中,当点E落在AB上时,BF的长最大,最大值=3![]()
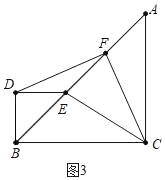
如图4中,当点E落在AB的延长线上时,BF的值最小,最小值=![]() .
.
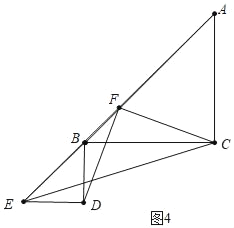
综上所述,![]() ≤BF≤3
≤BF≤3![]() .
.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.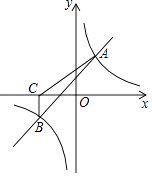
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式kx+b< ![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品A的零售价为每件900元,为了适应市场竞争,商店按零售价的九折优惠后,再让利40元销售,仍可获利10%.
(1)这种商品A的进价为多少元?
(2)现有另一种商品B进价为600元,每件商品B也可获利10%.对商品A和B共进货100件,要使这100件商品共获纯利6670元,则需对商品A、B分别进货多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,AE⊥EF,∠DEA=30°.

(1)求证:DC//AB.
(2)求∠AFE的大小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用二元一次方程组解决问题:近日由于城市地下水管老旧破裂,全市停水.小明去超市购买生活用水,已知大桶矿泉水每桶5升,价值10.5元,小瓶矿泉水每瓶500毫升,价值1.5元.(1升=1000毫升)
(1)若小明要购买1大桶矿泉水和3小瓶矿泉水,需要 元;
(2)若小明生活用水总量为20升,共花费46.5元,问这两种矿泉水各买多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们在过去的学习中已经发现了如下的运算规律:
(1)15×15=1×2×100+25=225;
(2)25×25=2×3×100+25=625;
(3)35×35=3×4×100+25=1225;
……
按照这种规律,第n个式子可以表示为
A. n×n=![]() ×(
×(![]() +1)×100+25=n2
+1)×100+25=n2
B. n×n=![]() ×(
×(![]() +1)×100+25=n2
+1)×100+25=n2
C. (n+5)×(n+5)=n×(n+1)×100+25=n2+10n+25
D. (10n+5)×(10n+5)=n×(n+l)×l00+25=100n2+100n+25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球.若红球个数是黑球个数的2倍多40个.从袋中任取一个球是白球的概率是![]() .
.
(1)求袋中红球的个数;
(2)求从袋中任取一个球是黑球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数表达式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,求点P的坐标;
②若△PQB的面积为![]() ,请直接写出点M的坐标.
,请直接写出点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com