
����Ŀ����ͼ1������ABCD�����������������ϣ���D������ԭ��O�غϣ���AD=8��AB=6����ͼ2������ABCD��OB������ÿ��1����λ���ȵ��ٶ��˶���ͬʱ��P��A�����Ҳ��ÿ��1����λ���ȵ��ٶ��ؾ���ABCD�ı�AB������B���C�˶�������P�����Cʱ������ABCD�͵�Pͬʱֹͣ�˶������P���˶�ʱ��Ϊt�룮
��1����t=5ʱ����ֱ��д����D����P�����ꣻ
��2������P���߶�AB���߶�BC���˶�ʱ�������PBD�����S����t�ĺ�����ϵʽ����д����Ӧt��ȡֵ��Χ��
��3����P���߶�AB���߶�BC���˶�ʱ����PE��x�ᣬ����Ϊ��E������PEO����BCD����ʱ�������Ӧ��tֵ��

���𰸡���1��D����4��3����P����12��8������2��![]() ����3��6��
����3��6��
�������������������1���ӳ�CD��x����M���ӳ�BA��x����N����CM��x�ᣬBN��x�ᣬAD��x�ᣬBN��DM���ɾ��ε����ʵó����ɶ������BD��BO=15����ƽ���ߵó���ABD�ס�NBO���ó�����ʽ![]() �����BN��NO���ó�OM��DN��PN�����ɵó���D��P�����ꣻ
�����BN��NO���ó�OM��DN��PN�����ɵó���D��P�����ꣻ
��2������P�ڱ�AB��ʱ��BP=6��t���������ε������ʽ�ó�S=![]() BPAD��������P�ڱ�BC��ʱ��BP=t��6��ͬ���ó�S=
BPAD��������P�ڱ�BC��ʱ��BP=t��6��ͬ���ó�S=![]() BPAB�����ɵó������
BPAB�����ɵó������
��3�����D��![]() ��
�� ![]() ���������������������P�ڱ�AB��ʱ��P��
���������������������P�ڱ�AB��ʱ��P��![]() ��
�� ![]() ������
������![]() ��
��![]() ʱ���ֱ����t��ֵ��
ʱ���ֱ����t��ֵ��
������P�ڱ�BC��ʱ��P��![]() ��
�� ![]() ������
������![]() ��
��![]() ʱ���ֱ����t��ֵ���ɣ�
ʱ���ֱ����t��ֵ���ɣ�
�����������1���ӳ�CD��x����M���ӳ�BA��x����N����ͼ1��ʾ����CM��x�ᣬBN��x�ᣬAD��x�ᣬBN��DM�����ı���ABCD�Ǿ��Σ����BAD=90����CD=AB=6��BC=AD=8����BD=![]() =10����t=5ʱ��OD=5����BO=15����AD��NO�����ABD�ס�NBO����
=10����t=5ʱ��OD=5����BO=15����AD��NO�����ABD�ס�NBO����![]() ����
����![]() ����BN=9��NO=12����OM=12��8=4��DM=9��6=3��PN=9��1=8��/span>��D����4��3����P����12��8����
����BN=9��NO=12����OM=12��8=4��DM=9��6=3��PN=9��1=8��/span>��D����4��3����P����12��8����
��2����ͼ2��ʾ������P�ڱ�AB��ʱ��BP=6��t����S=![]() BPAD=
BPAD=![]() ��6��t����8=��4t+24��
��6��t����8=��4t+24��
������P�ڱ�BC��ʱ��BP=t��6����S=![]() BPAB=
BPAB=![]() ��t��6����6=3t��18��
��t��6����6=3t��18��
���������� ![]() ��
��
��3����� D��![]() ��
�� ![]() ����
����
������P�ڱ�AB��ʱ��P��![]() ��
�� ![]() ������
������![]() ʱ��
ʱ��  ����ã�t=6��
����ã�t=6��
��![]() ʱ��
ʱ��  ����ã�t=20���������⣬��ȥ����
����ã�t=20���������⣬��ȥ����
������P�ڱ�BC��ʱ��P��![]() ��
�� ![]() ������
������![]() ʱ��
ʱ��  ����ã�t=6��
����ã�t=6��
��![]() ʱ��
ʱ��  ����ã�
����ã� ![]() ���������⣬��ȥ����
���������⣬��ȥ����
������������t=6ʱ����PEO����BCD���ƣ�




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A�������������£�72��73��76��76��77��78��78��B����������ǡ����A��������ÿ������2����A��B��������������ͳ������Ӧ��ͬ���ǣ�������
A. ƽ���� B. ���� C. ��λ�� D. ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1��26������7��+����16����3
��2��6+����2��3��5������3.2����4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��O�����������ABC��һ�㣬��AOB����BOC����COA��120����P�ǡ�ABC�ڲ�ͬ��O����һ�㣬��A��BO������A��BP��ֱ��ɡ�AOB����APB��ת���ã���ת�Ƕ�Ϊ60�㣬�����н�������ȷ����( )��(��ʾ����һ������60��ĵ����������ǵȱ�������)
�١�O��BOΪ�ȱ������Σ���A����O����O��C��һ��ֱ���ϣ�
��A��O����O��O��AO��BO�� ��A��P����P��P��PA��PB��
��PA��PB��PC>AO��BO��CO��
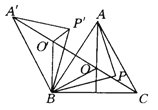
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
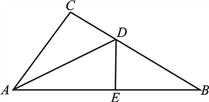
����Ŀ����ͼ����ֱ����ABC�У���C=90����DE��ֱƽ��AB����BC�ڵ�D����AB�ڵ�E��
��1����ADƽ����CAB�����B�Ķ����� �� ����
��2����AB=10����ACD���ܳ�Ϊ14������ACB���ܳ�.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com