
 如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.分析 (1)连结OA,利用r表示出OD的长,在Rt△AOD中根据勾股定理求出r的值即可;
(2)连结OA′,在Rt△A′EO中,由勾股定理得出A′E的长,进而可得出A′B′的长,据此可得出结论.
解答  解:(1)连结OA,
解:(1)连结OA,
由题意得:AD=$\frac{1}{2}$AB=30,OD=(r-18)
在Rt△ADO中,由勾股定理得:r2=302+(r-18)2,
解得,r=34;
(2)连结OA′,
∵OE=OP-PE=30,
∴在Rt△A′EO中,由勾股定理得:A′E2=A′O2-OE2,即:A′E2=342-302,
解得:A′E=16.
∴A′B′=32.
∵A′B′=32>30,
∴不需要采取紧急措施.
点评 本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.


科目:初中数学 来源: 题型:选择题
 如图,已知在△ABC中,cosA=$\frac{1}{3}$,BE、CF分别是AC、AB边上的高,联结EF,那么△AEF和△ABC的周长比为( )
如图,已知在△ABC中,cosA=$\frac{1}{3}$,BE、CF分别是AC、AB边上的高,联结EF,那么△AEF和△ABC的周长比为( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
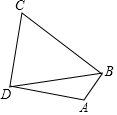 已知:在四边形ABCD中,∠ABC=90°,∠C=60,AB=$\frac{\sqrt{3}}{2}$,BC=1+$\sqrt{3}$,CD=2
已知:在四边形ABCD中,∠ABC=90°,∠C=60,AB=$\frac{\sqrt{3}}{2}$,BC=1+$\sqrt{3}$,CD=2查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com