
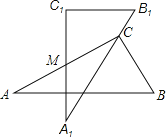
【题目】如图所示是两块完全一样的含30°角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,设较长直角边的中点为M,绕中点M转动三角板ABC,使其直角顶点C恰好落在三角板A1B1C1的斜边A1B1上,当∠A=30°,AC=10时,两直角顶点C,C1的距离是 .
科目:初中数学 来源: 题型:
【题目】如果10b=n,那么称b为n的劳格数,记为b=d (n),由定义可知:10b=n与b=d (n)所表示的是b、n两个量之间的同一关系.
(1)根据劳格数的定义,填空:d(10)= ,d(10﹣2)= ;
劳格数有如下运算性质:
若m、n为正数,则d(mn)=d(m)+d(n),d(![]() )=d(m)﹣d(n).
)=d(m)﹣d(n).
根据运算性质,填空:![]() = (a为正数).
= (a为正数).
(2)下表中与数x对应的劳格数d (x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.
x | 1.5 | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
d(x) | 3a﹣b+c | 2a﹣b | a+c | 1+a﹣b﹣c | 3﹣3a﹣3c | 4a﹣2b | 3﹣b﹣2c | 6a﹣3b |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】日前一名男子报警称,在菲律宾南部发现印有马来西亚国旗的飞机残骸,怀疑是失联的马航MH370客机,马来西亚警方立即派出直升机前去查证.飞机在空中A点看见残骸C的俯角为20°,继续沿直线AE飞行16秒到达B点,看见残骸C的俯角为45°,已知飞机的飞行度为3150米/分.
(参考数据:tan20°≈0.3,cos20°≈0.9,sin20°≈0.2)
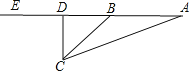
(1)求残骸到直升机航线的垂直距离CD为多少米?
(2)在B点时,机组人员接到总指挥部电话,8分钟后该海域将迎来比较大的风浪,为了能及时观察取证,机组人员决定飞行到D点立即空投设备,将残骸抓回机舱(忽略风速对设备的影响),己知设备在空中的降落与上升速度均为700米/分.设备抓取残骸本身需要6分钟,请问能否在风浪来临前将残骸抓回机舱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年12月6日,我县举行了2018年商品订货交流会,参加会议的每两家公司之间都签订了一份合同,所有参会公司共签订了28份合同,共有多少家公司参加了这次会议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个圆分割成三个扇形,它们的圆心角的度数之比为2:3:4,则这个扇形圆心角的度数为( )
A.30°,60°,90°
B.60°,120°,180°
C.50°,100°,150°
D.80°,120°,160°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合.
(1)若DE经过点C,DF交AC于点G,求重叠部分(△DCG)的面积;
(2)合作交流:“希望”小组受问题(1)的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,求重叠部分(△DGH)的面积.
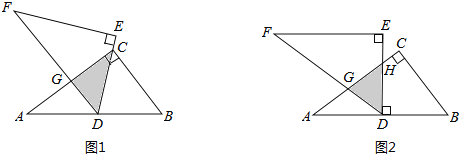
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个数的和是10,其中一个数用字母x表示,那么表示这两个数的积的代数式是( )
A. 10x B. x (10+x) C. x (10-x) D. x (x-10)
查看答案和解析>>
科目:初中数学 来源: 题型:
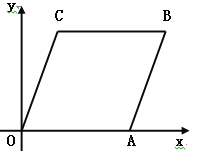
【题目】如图,在直角坐标系xoy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)写出点C的坐标;
(2)当△ODC的面积是△ABD的面积的3倍时,求点D的坐标;
(3)设∠OCD=α,∠DBA=β,∠BDC=θ,判断α、β、θ之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com