已知A(1,0)、B(0,-1)、C(-1,2)、D(2,-1)、E(4,2)五个点,抛物线y=a(x-1)2+k(a>0)经过其中的三个点.
(1)求证:C、E两点不可能同时在抛物线y=a(x-1)2+k(a>0)上;
(2)点A在抛物线y=a(x-1)2+k(a>0)上吗?为什么?
(3)求a和k的值.
解:(1)∵抛物线y=a(x-1)
2+k的对称轴为x=1,
而C(-1,2),E(4,2)两点纵坐标相等,
由抛物线的对称性可知,C、E关于直线x=1对称,
又∵C(-1,2)与对称轴相距2,E(4,2)与对称轴相距3,
∴C、E两点不可能同时在抛物线上;
(2)假设点A(1,0)在抛物线y=a(x-1)
2+k(a>0)上,
则a(1-1)
2+k=0,解得k=0,
因为抛物线经过5个点中的三个点,
将B(0,-1)、C(-1,2)、D(2,-1)、E(4,2)代入,
得出a的值分别为a=-1,a=

,a=-1,a=

,
所以抛物线经过的点是B,D,
又因为a>0,与a=-1矛盾,
所以假设不成立.
所以A不在抛物线上;
(3)将D(2,-1)、C(-1,2)两点坐标代入y=a(x-1)
2+k中,得
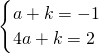
,
解得
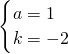
,
或将E、D两点坐标代入y=a(x-1)
2+k中,得
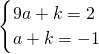
,
解得
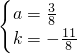
,
综上所述,
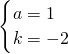
或
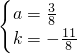
.
分析:(1)由抛物线y=a(x-1)
2+k可知,抛物线对称轴为x=1,而C(-1,2),E(4,2)两点纵坐标相等,应该关于直线x=1对称,但C(-1,2)与对称轴相距2,E(4,2)与对称轴相距3,故不可能;
(2)假设A点在抛物线上,得出矛盾排除A点在抛物线上;
(3)B、D两点关于对称轴x=1对称,一定在抛物线上,另外一点可能是C点或E点,分别将C、D或D、E两点坐标代入求a和k的值.
点评:本题考查了二次函数图象上点的坐标特点.关键是明确图象上点的坐标必须满足函数解析式.

 ,a=-1,a=
,a=-1,a= ,
,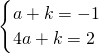 ,
,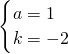 ,
,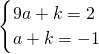 ,
,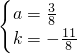 ,
,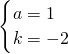 或
或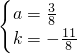 .
.

 4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.
4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.