练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，直线与双曲线相交于点A（m，3），与x轴交于点C．

    （1）求双曲线解析式；

    （2）点P在x轴上，如果△ACP的面积为3，求点P的坐标．

    （1）；（2）（﹣2，0）或（﹣6，0）． 【解析】试题分析：（1）把A坐标代入直线解析式求出m的值，确定出A坐标，即可确定出双曲线解析式； （2）设P（x，0），表示出PC的长，高为A纵坐标，根据三角形ACP面积求出x的值，确定出P坐标即可． 【解析】 （1）把A（m，3）代入直线解析式得：3=m+2，即m=2， ∴A（2，3）， 把A坐标代入y=，得k=6， ...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：云南省双柏县2017-2018学年上学期七年级期末数学试卷 题型：解答题

    甲乙两车分别相距360km的A，B两地出发，甲车的速度为65km/h，乙车的速度为55km/h．两车同时出发，相向而行，求经过多少小时后两车相距60 km．

    经过2.5h或3.5h后两车相距60 km． 【解析】试题分析：设xh后两车相距60km，然后分相遇前与相遇后两种情况列出方程求解即可． 试题解析：【解析】 设x h后两车相距60 km． 若相遇前，根据题意得，65x+65x=360-60，解得x=2.5； 若相遇后，根据题意得，65x+65x=360+60，解得x=3.5； 答：经过2.5h或3.5h后两车相距6...

    查看答案和解析>>

    科目：初中数学 来源：云南省双柏县2017-2018学年八年级上期期末数学试卷 题型：填空题

    计算： 的值是______________．

    -4 【解析】【解析】 =－4．故答案为：－4．

    查看答案和解析>>

    科目：初中数学 来源：江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型：填空题

    已知P是线段AB的黄金分割点，AP＞PB，AB＝2，则AP＝__________．

    -1 【解析】由于P为线段AB=2的黄金分割点， 且AP是较长线段； 则AP=2×.故答案为： .

    查看答案和解析>>

    科目：初中数学 来源：江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型：单选题

    如图，四边形ABCD内接于⊙O，AC平分∠BAD，则下列结论正确的是（　　）

    A. AB=AD B. BC=CD C. D. ∠BCA=∠DCA

    B 【解析】【解析】 ∵AC平分∠BAD， ∴∠BAC=∠DAC, ∴ , ∴BC=CD, 故选B

    查看答案和解析>>

    科目：初中数学 来源：山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型：填空题

    如图，Rt△AOB的一条直角边OB在x轴上，双曲线y=（x>0）经过斜边OA的中点C，与另一直角边交于点D．若S△OCD=9，则S△OBD的值为_______．

    6 【解析】试题分析：过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值，即S=|k|． 【解析】 如图，过C点作CE⊥x轴，垂足为E． ∵Rt△OAB中，∠OBA=90°， ∴CE∥AB， ∵C为Rt△OAB斜边OA的中点C， ∴CE为Rt△OAB的中位线， ∵△OEC∽△OBA， ∴=． ∵双曲线的...

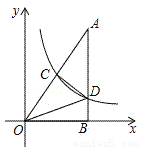
    查看答案和解析>>

    科目：初中数学 来源：山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型：单选题

    如图，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE，BF交于点G，将△BCF沿BF对折，得到△BPF，延长FP交BA延长线于点Q，下列结论正确的个数是（ ）

    ①AE=BF；②AE⊥BF；③sin∠BQP=；④S四边形ECFG=2S△BGE．

    A. 4 B. 3 C. 2 D. 1

    B 【解析】【解析】 ∵E，F分别是正方形ABCD边BC，CD的中点，∴CF=BE，在△ABE和△BCF中，∵AB=BC，∠ABE=∠BCF，BE=CF，∴Rt△ABE≌Rt△BCF（SAS），∴∠BAE=∠CBF，AE=BF，故①正确； 又∵∠BAE+∠BEA=90°，∴∠CBF+∠BEA=90°，∴∠BGE=90°，∴AE⊥BF，故②正确； 根据题意得，FP=FC，∠PFB...

    查看答案和解析>>

    科目：初中数学 来源：北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型：解答题

    计算：

    （）．

    （）．

    （）．

    （）．

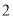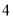    （1）1（2）-6（3）-20（4）17 【解析】试题分析：（1）原式从左到右依次计算即可得到结果； （2）原式利用减法法则变形，相加即可得到结果； （3）原式先计算乘方运算，再利用乘法分配律计算，最后算加减运算即可得到结果； （4）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果． 试题解析：（） ． （） ． （） ． （...

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

    如图，点A，B，C在同一直线上，在这条直线同侧作等边△ABD和等边△BCE，连接AE和CD，交点为M，AE交BD于点P，CD交BE于点Q，连接PQ、BM， 有4个结论：①△ABE≌△DBC，②△DQB≌△ABP，③∠EAC=30°，④∠AMC=120°，请将所有正确结论的序号填在横线上______.

    ①②④ 【解析】∵等边△ABD，等边△EBC，∴AB=BD=AD，BE=BC=EC，∠ABD=∠EBC=60°， ∴∠ABE=∠DBC，∠DBE=60°， 在△ABE和△DBC中， ， ∴△ABE≌△DBC，①说法正确； 由①可得：∠PAB=∠QDB， 在△DQB和△ABP中， ， ∴△DQB≌△ABP，②说法正确； ③说法不能证明，错误...

    查看答案和解析>>

    同步练习册答案