
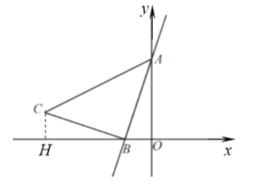
【题目】如图1,已知直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于A,B两点,过点B在第二象限内作
轴分别交于A,B两点,过点B在第二象限内作![]() 且
且![]() ,连接
,连接![]() .
.
(1)求点C的坐标.
(2)如图2,过点C作直线![]() 轴交AB于点D,交
轴交AB于点D,交![]() 轴于点E,
轴于点E,
请从下列A,B两题中任选一题作答,我选择______题
A.①求线段CD的长.
②在坐标平面内,是否存在点M(除点B外),使得以点M,C,D为顶点的三角形与![]() 全等?若存在,请直接写出所有符合条件的点M的坐标:若不存在,请说明理由.
全等?若存在,请直接写出所有符合条件的点M的坐标:若不存在,请说明理由.
B.①如图3,在图2的基础上,过点D作![]() 于点F,求线段DF的长.
于点F,求线段DF的长.
②在坐标平面内,是否存在点M(除点F外),使得以点M,C,D为顶点的三角形与![]() 全等?若存在,请直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
全等?若存在,请直接写出所有符合条件的点M的坐标;若不存在,请说明理由.

【答案】(1)C(-4,1);(2)A:①![]() ;②
;②![]() ;B:①
;B:①![]() ;②
;②![]()
【解析】
(1)首先由直线解析式求得点A、B的坐标,再从点C向x轴作垂线,证明三角形全等,由此求得点C的坐标;(2)选择A时,①由![]() 轴,知点D的纵坐标,代入一次函数解析式即可求得横坐标,由此得到线段CD的长;②利用轴对称可得到点M的坐标;选择B时,①求出线段AC的长,再利用△ACD的面积就可求得DF的长度;②利用轴对称可得到点M的坐标
轴,知点D的纵坐标,代入一次函数解析式即可求得横坐标,由此得到线段CD的长;②利用轴对称可得到点M的坐标;选择B时,①求出线段AC的长,再利用△ACD的面积就可求得DF的长度;②利用轴对称可得到点M的坐标
解:(1)在![]() 中,当
中,当![]() 时,
时,![]() ,
,
![]() 点A的坐标为(
点A的坐标为(![]()
在![]() 中,当
中,当![]() 时,
时,![]() ,
,
∴点B的坐标为![]() ,
,
![]()
过点C作![]() 轴于点H,则
轴于点H,则![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 点C在第二象限,
点C在第二象限,
![]() 点C的坐标为
点C的坐标为![]()
(2)A.①由(1)知点C的坐标为![]() ,
,
![]() 轴交AB于点D,
轴交AB于点D,![]() 点D的纵坐标为1,
点D的纵坐标为1,
将![]() 代入
代入![]() 得
得![]() ,
,
![]()
![]() 点D的坐标为
点D的坐标为![]() ,
,
![]()
②存在
当点M1与点B关于直线CD对称时,得点M1坐标为(-1,2);
当点M2与点B关于CD的垂直平分线对称时,得点M2坐标为![]() ;
;
当点M3与点点M2关于直线CD对称时,得点M3坐标为![]()
综上,当满足![]() 时,以点M,C,D为顶点的三角形与
时,以点M,C,D为顶点的三角形与![]() 全等
全等
B.①由(1)知点C的坐标为![]() ,
,
![]() 轴交AB于点D,交
轴交AB于点D,交![]() 轴于点E,
轴于点E,
![]() 点D的纵坐标为1,
点D的纵坐标为1,![]()
将![]() 代入
代入![]() 得
得![]()
![]() 点D的坐标为
点D的坐标为![]() ,
,
![]()
在![]() 中,
中,![]() ,
,
由勾股定理得![]() ,
,
![]()
∴![]()
![]()
![]()
![]()
②存在
在Rt△CDF中,由勾股定理得![]()
∵![]()
∴![]()
即点F为线段AC靠近点A的一个三等分点,∴F(![]()
当点M1与点F关于直线CD对称时,点M1坐标为![]()
当点M2与点F关于线段CD的垂直平分线对称时,点M2坐标为![]() ;
;
当点M3与点F关于直线CD对称时,点M3坐标为![]()
综上,当满足![]() 时,以点M,C,D为顶点的三角形与
时,以点M,C,D为顶点的三角形与![]() 全等
全等


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】求代数式a+![]() 的值,其中a=1007
的值,其中a=1007
如图是小亮和小芳的解答过程:

(1) 的解法是错误的;
(2)错误的原因在于未能正确的运用二次根式的性质: ;
(3)求代数式a+2![]() 的值,其中a=﹣2019.
的值,其中a=﹣2019.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°,连接AC.
(1)△ACD是直角三角形吗?为什么?
(2)小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+3和x轴、y轴的交点分别为B、C,∠OBC=30°,点A的坐标是(![]() ,0),另一条直线经过点A、C.
,0),另一条直线经过点A、C.
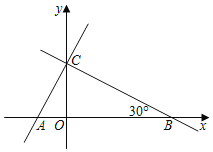
(1)求点B的坐标及k的值;
(2)求证:AC⊥BC;
(3)点M为直线BC上一点(与点B不重合),设点M的横坐标为x,△ABM的面积为S.
①求S与x的函数关系式;
②当S=6![]() 时,求点M的坐标.
时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年10月1日是中华人民共和国成立70周年纪念日,红色旅游成为旅游热点.小王要和朋友们去某红色景点旅游,其门票零售价为80元/张.国庆节期间,景点推出优惠活动,方案1:门票一律九折优惠;方案2:对10人以内(含10人)购门票不优惠,超过10人超出部分八折优惠.设小王一行参加旅游的人数为x(人),购买门票费用为y(元).
(1)小王分别写出方案1和方案2购买门票的费用y(元)与旅游人数x(人)之间的函数表达式如下,请你将空缺部分补充完整:
![]() ______
______![]() ;
;![]()
(2)小王一行共有40人一起去该景点旅游,通过计算,判断选择哪种方案更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则点Bn的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在Rt△ABC中,∠C=90°,AC=BC=![]() ,直线L过AB中点O,过点A、C分别向直线L作垂线,垂足分别为E、F.若CF=1,则EF=__.
,直线L过AB中点O,过点A、C分别向直线L作垂线,垂足分别为E、F.若CF=1,则EF=__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com