
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | |
| 路程(千米) | 30 | 33 | 27 | 37 | 35 | 53 | 30 |
分析 (1)先利用平均数的计算公式求出每天行驶的路程,再乘以总天数即可.
(2)根据每月要行驶的距离求出每年要行驶的距离,再乘以耗油量和价格就可求出一年的汽油费用.
解答 解:(1)根据题意得:
$\frac{1}{7}$(30+35+27+37+35+53+30)=35(千米),35×30=1050(千米),
答:此人的轿车每月(按30天计算)约行驶1050千米;
(2)根据题意得:
1050×12÷100×6.70=6753.6(元)
答:此人一年(按12个月计算)的汽油费用大约是6753.6元.
点评 本题考查用样本估计总体及算术平均数的知识,平均数的计算方法是求出所有数据的和,然后除以数据的总个数.用样本估计总体的思想方法要会运用.


科目:初中数学 来源: 题型:解答题
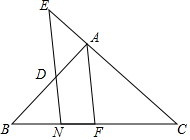 如图,在△ABC中,直线DN平行于中线AF交AB于点D,交AC的延长线于点E,交边BC于点N,求证:$\frac{AD}{AB}$=$\frac{AE}{AC}$.
如图,在△ABC中,直线DN平行于中线AF交AB于点D,交AC的延长线于点E,交边BC于点N,求证:$\frac{AD}{AB}$=$\frac{AE}{AC}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
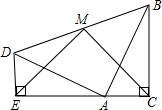 两个全等的含30°,60°角的三角板ADE和三角板ABC如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的中点M,连接ME,MC.试判断线段ME和线段MC之间的关系,并说明理由.
两个全等的含30°,60°角的三角板ADE和三角板ABC如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的中点M,连接ME,MC.试判断线段ME和线段MC之间的关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com