
【题目】在Rt△ABC中,∠C=90°,在下列条件中不能解直角三角形的是( )
A. 已知a和A B. 已知c和b
C. 已知A和B D. 已知a和B
科目:初中数学 来源: 题型:
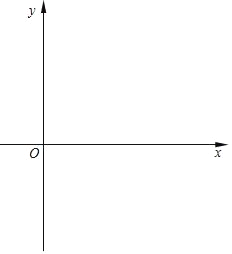
【题目】在平面直角坐标系中,已知抛物线y=ax2+bx+c(a>0)与x轴交于A(﹣1,0)、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D,对称轴为直线x=1,交x轴于点E,tan∠BDE=![]() .
.
(1)求抛物线的表达式;
(2)若点P是对称轴上一点,且∠DCP=∠BDE,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】即墨素有“中国针织名城”的美誉,2016年,又被中国服装协会授予“中国童装名称”的称号,该区一网店销售某款童装,当每件售价80元时,每周可卖200件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖20件.已知该款童装每件成本价60元,设该款童装每件售价x(60≤x≤80)元,每周的销售量为y件.
(1)求y与x之间的函数关系式;
(2)设每周的销售利润为W元,当每件售价定为多少元时,每周的销售利润最大,最大利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
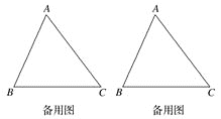
【题目】如图1,给定锐角三角形ABC,小明希望画正方形DEFG,使D,E位于边BC上,F,G分别位于边AC,AB上,他发现直接画图比较困难,于是他先画了一个正方形HIJK,使得点H,I位于射线BC上,K位于射线BA上,而不需要求J必须位于AC上.这时他发现可以将正方形HIJK通过放大或缩小得到满足要求的正方形DEFG.
阅读以上材料,回答小明接下来研究的以下问题:
(1)如图2,给定锐角三角形ABC,画出所有长宽比为2:1的长方形DEFG,使D,E位于边BC上,F,G分别位于边AC,AB上.
(2)已知三角形ABC的面积为36,BC=12,在第(1)问的条件下,求长方形DEFG的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
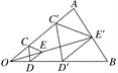
【题目】如图,用下面的方法可以画△AOB的内接等边三角形,阅读后解答相应问题.
画法:①在△AOB内画等边三角形CDE,使点C在OA上,点D在OB上;②连接OE并延长,交AB于点E′,过点E′作E′C′∥EC,交OA于点C′,作E′D′∥ED,交OB于点D′;③连接C′D′,则△C′D′E′是△AOB的内接等边三角形.
(1)求证:△C′D′E′是等边三角形;
(2)求作:内接于已知△ABC的矩形DEFG,使它的边EF在BC上,顶点D,G分别在AB,AC上,且DE:EF=1∶2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AB=4,BC=5,CA=6.
(1)如果DE=10,那么当EF=________,FD=________时,△DEF∽△ABC;
(2)如果DE=10,那么当EF=________,FD=________时,△FDE∽△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
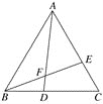
【题目】如图所示,△ABC是等边三角形,点D、E分别在BC、AC上,且CE=BD,BE、AD相交于点F.求证:
(1)△ABD≌△BCE;
(2)△AEF∽△ABE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ACB中,∠C=90°,AC=BC,一直角三角板的直角顶角O在AB边的中点上,这块三角板绕O点旋转,两条直角边始终与AC、BC边分别相交于E、F,连接EF,则在运动过程中,△OEF与△ABC的关系是( )
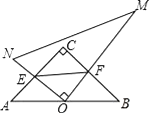
A. 一定相似 B. 当E是AC中点时相似
C. 不一定相似 D. 无法判断
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com