
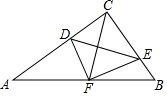
 如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为$\frac{25}{8}$.
如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为$\frac{25}{8}$. 分析 根据D,C,E,F四点共圆,可得∠CDE=∠CFE=∠B,再根据CE=FE,可得∠CFE=∠FCE,进而根据∠B=∠FCE,得出CF=BF,同理可得CF=AF,由此可得F是AB的中点,求得CF=$\frac{1}{2}$AB=5,再判定△CDF∽△CFA,得到CF2=CD×CA,进而得出CD的长.
解答  解:由折叠可得,∠DCE=∠DFE=90°,
解:由折叠可得,∠DCE=∠DFE=90°,
∴D,C,E,F四点共圆,
∴∠CDE=∠CFE=∠B,
又∵CE=FE,
∴∠CFE=∠FCE,
∴∠B=∠FCE,
∴CF=BF,
同理可得,CF=AF,
∴AF=BF,即F是AB的中点,
∴Rt△ABC中,CF=$\frac{1}{2}$AB=5,
由D,C,E,F四点共圆,可得∠DFC=∠DEC,
由∠CDE=∠B,可得∠DEC=∠A,
∴∠DFC=∠A,
又∵∠DCF=∠FCA,
∴△CDF∽△CFA,
∴CF2=CD×CA,即52=CD×8,
∴CD=$\frac{25}{8}$,
故答案为:$\frac{25}{8}$.
点评 本题主要考查了折叠问题,四点共圆以及相似三角形的判定与性质的运用,解决问题的关键是根据四点共圆以及等量代换得到F是AB的中点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
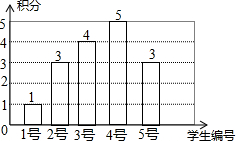 编号为1~5号的5名学生进行定点投篮,规定每人投5次,每命中1次记1分,没有命中记0分,如图是根据他们各自的累积得分绘制的条形统计图.之后来了第6号学生也按同样记分规定投了5次,其命中率为40%.
编号为1~5号的5名学生进行定点投篮,规定每人投5次,每命中1次记1分,没有命中记0分,如图是根据他们各自的累积得分绘制的条形统计图.之后来了第6号学生也按同样记分规定投了5次,其命中率为40%.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A,B两点.若点A的坐标为(n,1),则k的值为$\frac{\sqrt{5}-1}{2}$.
如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A,B两点.若点A的坐标为(n,1),则k的值为$\frac{\sqrt{5}-1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
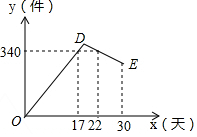 某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.
某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com