练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

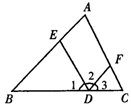
    如图5所示，

       ①因为∠1=∠C（已知），所以ED∥______．（__________）

       ②因为∠2=∠BED（已知），所以DF∥_______．（_________）

       ③因为∠3=∠B（已知），所以_____∥______（__________）

       ④因为∠2+∠AFD=180°（已知），所以_____∥______．（__________）

       ⑤因为∠DFC=∠C_____（已知），所以ED∥AC．（_________）

    ①AC  同位角相等，两直线平行 

    ②AB  内错角相等，两直线平行 

    ③DF  AB  同位角相等，两直线平行 

    ④DE  AC  同旁内角互补，两直线平行 

    ⑤2  内错角相等，两直线平行 

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图1，已知等边△ABC的边长为1，D、E、F分别是AB、BC、AC边上的点（均不与点A、B、C重合），记△DEF的周长为p．
    （1）若D、E、F分别是AB、BC、AC边上的中点，则p=
     
    ；
    （2）若D、E、F分别是AB、BC、AC边上任意点，则p的取值范围是
     
    ．
    小亮和小明对第（2）问中的最小值进行了讨论，小亮先提出了自己的想法：将△ABC以AC边为轴翻折一次得△AB1C，再将△AB1C以B1C为轴翻折一次得△A1B1C，如图2所示．则由轴对称的性质可知，DF+FE1+E1D2=p，根据两点之间线段最短，可得p≥DD2．老师听了后说：“你的想法很好，但DD2的长度会因点D的位置变化而变化，所以还得不出我们想要的结果．”小明接过老师的话说：“那我们继续再翻折3次就可以了”．请参考他们的想法，写出你的答案．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•如东县一模）图1是一个底面为正方形的直棱柱金属块，因设计需要将它切去一角，如图2所示，则切去后金属块的俯视图是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （A卷）美化城市，改善人们的居住环境已成为城市建设的一项重要内容．我市近几年来，通过拆迁旧房，植草，栽树，修公园等措施，使城区绿地面积不断增加（如图1所示）．
    （1）根据图中所提供的信息回答下列问题：2003年底的绿地面积为
    60
    60
    公顷，比2002年底增加了
    4
    4
    公顷；在2001年，2002年，2003年这三个中，绿地面积增加最多的是
    2002
    2002
    年；
    （2）为满足城市发展的需要，计划到2005年底使城区绿地面积达到72.6公顷，试求今明两年绿地面积的年平均增长率．

    （B 卷）2009年5月17日至21日，甲型H1N1流感在日本迅速蔓延，每天的新增病例和累计确诊病例人数如图2所示．
    （1）在5月17日至5月21日这5天中，新增甲型H1N1流感病例最多的是哪一天？该天增加了多少人？
    （2）在5月17日至5月21日这5天中，平均每天新增加甲型H1N1流感确诊病例多少人？如果接下来的5天中，继续按这个平均数增加，那么到5月26日，甲型H1N1流感累计确诊病例将会达到多少人？
    （3）甲型H1N1流感病毒的传染性极强，某地因1人患了甲型H1N1流感没有及时隔离治疗，经过两天传染后共有9人患了甲型H1N1流感，每天传染中平均一个人传染了几个人？如果按照这个传染速度，再经过5天的传染后，这个地区一共将会有多少人患甲型H1N1流感？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    图1是一个底面为正方形的直棱柱金属块，因设计需要将它切去一角，如图2所示，则切去后金属块的俯视图是                     （   ）

         

     

    查看答案和解析>>

    科目：初中数学 来源：2011届河南省周口市初三下学期第二十八章二次函数图像与性质检测题 题型：解答题

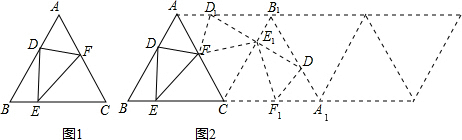
    如图1，已知等边△ABC的边长为1，D、E、F分别是AB、BC、AC边上的点（均不与点A、B、C重合），记△DEF的周长为.

    （1）若D、E、F分别是AB、BC、AC边上的中点，则=_______；
    （2）若D、E、F分别是AB、BC、AC边上任意点，则的取值范围是            .
    小亮和小明对第（2）问中的最小值进行了讨论，小亮先提出了自己的想法：将以AC边为轴翻折一次得，再将以为轴翻折一次得，如图2所示. 则由轴对称的性质可知，，根据两点之间线段最短，可得. 老师听了后说：“你的想法很好，但的长度会因点D的位置变化而变化，所以还得不出我们想要的结果.”小明接过老师的话说：“那我们继续再翻折3次就可以了”.请参考他们的想法，写出你的答案.

    查看答案和解析>>

    同步练习册答案