练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在△ABC中，∠B=30°，AB的垂直平分线交BC于E，交AB于D，连接AE，若AE平分∠BAC，BE=4，则CE的长为（ ）

    A. 8 B. 6 C. 4 D. 2

    D 【解析】∵DE垂直平分AB，∴BE=AE=4，∴∠A=∠BAE=30°， ∵AE平分∠BAC，∴∠BAE=∠EAC=30°，∴∠BAC=60°， ∴∠C=90°，∴EC=AE=2. 故选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型：填空题

    如图，抛物线y=ax2+bx+c（a＞0）的对称轴是过点（1，0）且平行于y轴的直线，若点P（4，0）在该抛物线上，则4a﹣2b+c的值为_________．

    0 【解析】试题分析：设抛物线与x轴的另一个交点是Q，∵抛物线的对称轴是过点（1，0），与x轴的一个交点是P（4，0），∴与x轴的另一个交点Q（﹣2，0），把（﹣2，0）代入解析式得：0=4a﹣2b+c，∴4a﹣2b+c=0，故答案为：0．

    查看答案和解析>>

    科目：初中数学 来源：天津市2018届九年级（上）第四周周清数学试卷 题型：解答题

    已知二次函数的图象与x轴的两个交点坐标是（﹣3，0）和（4，0），这个函数也过点（6，18），求这个二次函数的解析式．

    y=x2﹣x﹣12 【解析】试题分析：设二次函数的解析式为y=ax2+bx+c（a≠0），再把函数的图象与x轴的两个交点坐标以及点（6，18）代入求出a，b，c的值即可． 试题解析：设二次函数的解析式为y=ax2+bx+c（a≠0）． 根据题意，得， 解得： ， ∴二次函数的解析式为y=x2﹣x﹣12．

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    如图，△ABC中，AB=AC，作AD⊥BC，CE⊥AB，垂足分别为D，E，AD和CE相交于点F，若已知AE=CE.

    (1)求证：△AEF≌△CEB；

    (2)求证：AF=2CD

    （1）证明见解析；（2）证明见解析. 【解析】试题分析：（1）要证明△AEF≌△CEB，已知条件有AE=EC，∠AEF=∠BEC=90°，还差一个条件，由AD⊥BC，CE⊥AB可得∠B+∠BAD=90°，∠B+∠BCE=90°，所以得出∠EAF=∠ECB，因此可证明出△AEF≌△CEB；（2）由（1）结论可得：AF=BC，即要证明BC=2CD，由等腰三角形三线合一性质不难证明. 试题解...

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

    如图，△AEB≌△DFC，AE⊥CB，DF⊥BC，垂足分别为E、F，且AE=DF，若∠C=28°，则∠A=__________.

    62° 【解析】∵△AEB≌△DFC，∴∠C=∠B=28°， ∵AE⊥CB，∴∠AEB=90°，∴∠A=62°. 故答案为62°.

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型：单选题

    若一个三角形三个内角度数的比为1:2:3，则其内角度数最大的是（ ）

    A. 60° B. 90° C. 120° D. 无法判断

    B 【解析】设这三个角的度数分别为：x，2x，3x，所以x+2x+3x=180，解得x=30， 所以角度最大的为3x=90°. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：江苏省东部分校2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    一次函数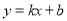的图象过点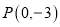，与函数的图象相交于．

    （1）求的值；

    （2）若函数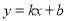的图象与轴的交点是B，函数的图象与轴的交点是C，与x轴交于点Ｄ，求三角形ABD的面积（其中O为坐标原点）．

    (1)a=,k=2,b=-3;(2) . 【解析】试题分析：（1）根据一次函数y=kx+b的图象与函数的图象相交于点，先求a的值， （2）再把A、P两点的坐标代入一次函数y=kx+b中，求得k、b的值，再由题意求得B、C两点的坐标，从而求出四边形ABOC的面积 试题解析： （1）由题意将A坐标代入得：a＝×+1＝ （2）∵直线y=kx+b过点P(0，?3)，A(，)，...

    查看答案和解析>>

    科目：初中数学 来源：江苏省东部分校2017-2018学年八年级上学期期末考试数学试卷 题型：单选题

    已知无论n取什么实数，点P（n, 4n-3）都在直线l上，若Q（a， b）是直线l上的点，则4a-b的平方根等于（　　）

    A. B. 1 C. D.

    D 【解析】试题解析：∵令n=0，则P（0，-3）；再令n=1，则P（1，1），由于n不论为何值此点均在直线l上， ∴设此直线的解析式为y=kx+b（k≠0）， ∴， 解得， ∴此直线的解析式为：y=4x-3， ∵Q（a，b）是直线l上的点， ∴4a-3=b，即4a-b=3， ∴4a-b的平方根等于 故选D.

    查看答案和解析>>

    科目：初中数学 来源：江西省萍乡市2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

    用同样大小的黑色棋子按如图所示的规律摆放：

    则第5个图案有____个棋子，第n个图案有____个棋子．（用含n的式子表示）

    18 3n+3． 【解析】试题解析：∵第1个图形有6个棋子， 第2个图形有6+3=9个棋子， 第3个图形有6+3×2=12个棋子， 第4个图形有6+3×4=18个棋子， ∴第5个图形有18个棋子， ∴第n个图形有棋子(3n+3)个[或6+3(n?1)等]. 故答案为：18，3n+3.

    查看答案和解析>>

    同步练习册答案