练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    （1）请用“＞”、“＜”、“=”填空：
    ①32+22______2×3×2
    ②52+52______2×5×5
    ③（
    		3
    ）2+（
    		2
    ）2______2×
    		3
    ×
    		2

    ④（-6）2+32______2×（-6）×3
    ⑤（-2）2+（-2）2______2×（-2）×（-2）
    （2）观察以上各式，请猜想a2+b2与2ab的大小；
    （3）你能借助于完全平方公式证明你的猜想吗？试试看！
    （1）①32+22=13，2×3×2=12，
    故32+22＞2×3×2，
    ②52+52=20，2×5×5=20，
    故52+52=2×5×5，
    ③（
    		3
    ）2+（
    		2
    ）2=5=
    		25
    ，2×
    		3
    ×
    		2
    =
    		24
    ，
    故（
    		3
    ）2+（
    		2
    ）2＞2×
    		3
    ×
    		2
    ，
    ④（-6）2+32=45，2×（-6）×3=-36，
    故（-6）2+32＞2×（-6）×3，
    ⑤（-2）2+（-2）2=8，2×（-2）×（-2）=8，
    故（-2）2+（-2）2=2×（-2）×（-2）；

    （2）a2+b2≥2ab；

    （3）∵（a-b）2≥0，
    ∴a2-2ab+b2≥0，
    即a2+b2≥2ab．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2013•滨湖区二模）一不透明的袋子中装有4个球，它们除了上面分别标有的号码1、2、3、4不同外，其余均相同．将小球搅匀，并从袋中任意取出一球后放回；再将小球搅匀，并从袋中再任意取出一球．若把两次号码之和作为一个两位数的十位上的数字，两次号码之差的绝对值作为这个两位数的个位上的数字，请用“画树状图”或“列表”的方法求所组成的两位数是奇数的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网某餐厅为了开展促销活动，设立一个可以自由转动的转盘（如图，转盘被分成四等份）．规定凡在本餐厅就餐的顾客，可以连续转动转盘两次，如果两次指针指向同一个汉字所在区域，即可获得一份礼物．请用画树状图（或列表）的方法，求顾客连续转动转盘两次能获得礼物的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

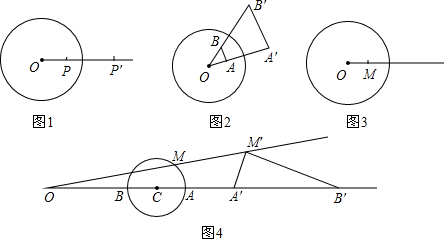
    （2013•江东区模拟）数学家已证明“不能用直尺和圆规三等分角”．如果不限作图工具呢？有位数学爱好者制作了如下的“三等分角器”；将量角器直径BC和一条直尺AB放在同一条直线上，移动量角器使得AB=OB=OC，另一条直尺的边缘BD过点B，且BD⊥AB，并用固件按这样的位置固定．
    （1）如图，把∠MPN的顶点P放在三等分角器的BD线上，移动器具，使∠MPN的一边MP过点A，另一边PN和半圆相切．请你说明直线PB和PO三等分∠MON．
    （2）若从量角器上读的∠COE=x（0＜x＜90°）请用含x的代数式表示∠MPN的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在不透明的口袋里装有白、红两种颜色的乒乓球（除颜色外其余都相同），其中白球有2个，红球1个．
    （1）搅匀后，若从中摸出两个球，请用画树状图或列表格法，求摸到的两个球都是白球的概率．
    （2）搅匀后从中任意摸出一个球，要使摸出红球的概率是
    23
    ，应如何添加红球？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•浙江一模）如图1，在平面上，给定了半径为r的⊙O，对于任意点P，在射线OP上取一点P′，使得OP•OP′=r2，这种把点P变为点P′的变换叫做反演变换，点P与点P′叫做互为反演点，⊙O称为基圆．
    （1）如图2，⊙O内有不同的两点A、B，它们的反演点分别是A′、B′，则与∠A′一定相等的角是
    （C）
    （C）

    （A）∠O         （B）∠OAB        （C）∠OBA           （D）∠B′
    （2）如图3，⊙O内有一点M，请用尺规作图画出点M的反演点M′；（保留画图痕迹，不必写画法）．
    （3）如果一个图形上各点经过反演变换得到的反演点组成另一个图形，那么这两个图形叫做互为反演图形．已知基圆O的半径为r，另一个半径为r1的⊙C，作射线OC交⊙C于点A、B，点A、B关于⊙O的反演点分别是A′、B′，点M为⊙C上另一点，关于⊙O的反演点为M′．求证：∠A′M′B′=90°．

    查看答案和解析>>

    同步练习册答案