
(11分)如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.

(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,若四边形AODE是平行四边形,求点D的坐标.
(3)联接BC交x轴于点F.y轴上是否存在点P,使得△POC与△BOF相似?若存在,求出点P的坐标;若不存在,请说明理由.
(1)y=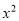 +2x;(2)D(1,3);(3)(0,-
+2x;(2)D(1,3);(3)(0,-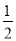 )或(0,-4)
)或(0,-4)
【解析】
试题分析:(1)将点A、点B和原点代入解析式进行求解;(2)根据平行四边形的性质得出点D的坐标;(3)首先求出OB、OF、OC的长度,然后根据三角形相似的条件求出点P的坐标,分两种情况进行讨论.
试题解析:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),
将点A(﹣2,0),B(﹣3,3),O(0,0),代入可得: ,解得:
,解得: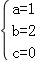 ,
,
所以函数解析式为:y=x2+2x;
(2)∵AO为平行四边形的一边, ∴DE∥AO,DE=AO, ∵A(﹣2,0),
∴DE=AO=2, ∵四边形AODE是平行四边形, ∴D在对称轴直线x=﹣1右侧,
∴D横坐标为:﹣1+2=1,代入抛物线解析式得y=3, ∴D的坐标为(1,3);
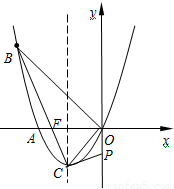
(3)在y轴上存在点P,使得△POC与△BOF相似,理由如下:
由y=x2+2x,顶点C的坐标为(﹣1,1) ∵tan∠BOF=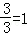 ,
,
∴∠BOF=45°, 当点P在y轴的负半轴时,tan∠COP=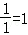 ,
,
∴∠COP=45°,∴∠BOF=∠COP, 设BC的解析式为y=kx+b(k≠0),
∵图象经过B(﹣3,3),C(﹣1,1)
∴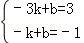 , 解得∴
, 解得∴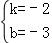 ,
,
∴y=﹣2x﹣3; 令y=0,则x=﹣1.5.
∴F(﹣1.5,0),
∴OB=3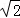 ,OF=1.5,OC=
,OF=1.5,OC=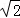 ,
,
①当△POC∽△FOB时, 则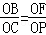 ,
,
即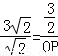 , ∴OP=
, ∴OP=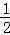 , ∴P(0,﹣
, ∴P(0,﹣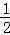 )
)
②当△POC∽△BOF时, ∴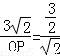 ,
,
∴OP=4, ∴P(0,﹣4),
∴当△POC与△BOF相似时,点P的坐标为(0,﹣ )或(0,﹣4).
)或(0,﹣4).
考点:待定系数法求函数解析式、三角形相似的判定、平行四边形的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年浙江省金华市青春共同体九年级上学期期中考试数学试卷(解析版) 题型:选择题
把一个小球以20米/秒的速度竖起向上弹出,它在空中的高度h(米)与时间t(秒),满足关系h=20t-5t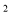 ,当小球达到最高点时,小球的运动时间为( )
,当小球达到最高点时,小球的运动时间为( )
A.1秒 B. 2秒 C.4秒 D.20秒
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省潍坊地区九年级上学期期末质量评估数学试卷(解析版) 题型:选择题
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
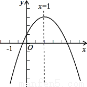
①abc<0;②b>a+c;③2a-b=0;④b2-4ac<0.其中正确的结论个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省潍坊地区九年级上学期期末质量评估数学试卷(解析版) 题型:选择题
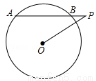
如图,⊙O的半径是4,点P是弦AB延长线上的一点,连接OP,若OP=6,∠APO=30°,则弦AB的长为( )
A.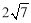 B.
B.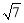 C.5 D.
C.5 D.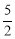
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省南阳市九年级上期期末摸底数学试卷(解析版) 题型:解答题
(9分)某工厂生产的某种产品按质量分为10个档次,第一档次(最低档次)的产品一天可生产80件,每件产品的利润为10元,每提高一个档次,每件产品的利润增加2元.
(1)当每件产品的利润为16元时,此产品质量在第几档次?
(2)由于生产工序不同,此产品每提高一个档次,一天的产量减少4件.若生产某档次产品一天的总利润为1200元,问该工厂生产的是第几档次的产品?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省南阳市九年级上期期末摸底数学试卷(解析版) 题型:填空题
如下图,在△ABC中,∠B=30°,点P是AB上一点,AP=2BP,PQ⊥BC于Q,连接AQ,则cos∠AQC的值为_________.
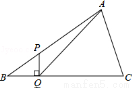
查看答案和解析>>
科目:初中数学 来源:2014-2015学年甘肃省白银市会宁县九年级上学期期末考试数学试卷(解析版) 题型:解答题
反比例函数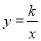 的图象与一次函数y=mx+b的图象交于A(1,3),B(n,-1)两点.
的图象与一次函数y=mx+b的图象交于A(1,3),B(n,-1)两点.
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当 取何值时,反比例函数的值大于一次函数的值.
取何值时,反比例函数的值大于一次函数的值.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年内蒙古包头市九年级上学期期末考试数学试卷(解析版) 题型:解答题
(本小题满分10分)如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC。
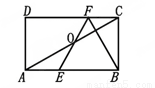
(1)求证:OE=OF;(2)若BC=2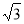 ,求AB的长。
,求AB的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com