
【题目】“五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过200元后的价格部分打七折;乙店一次性购物中超过500元后的价格部分打五折,设商品原价为x元(x≥0),购物应付金额为y元.
(1)求在甲商店购物时y与x之间的函数关系;
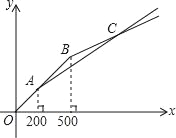
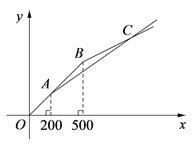
(2)两种购物方式对应的函数图象如图所示,求交点C的坐标;
(3)根据图象,请直接写出“五一”期间选择哪家商店购物更优惠.
【答案】(1)当0≤x≤200时,y1=x,当x>200时,y1=0.7x+60;(2)点C坐标(950,725);(3)见解析.
【解析】
(1)根据题意分当0≤x≤200时,当x>200时两种情况分别求出y1即可.
(2)求出直线BC,列方程组即可解决问题.
(3)利用图象即可解决问题.
解:(1)根据题意,得
当0 ≤ x ≤ 200时,y1=x;
当x > 200时,y1=200+0.7(x- 200)
=0.7 x+60.
综上所知,甲商店购物时y1与x之间的函数关系式为
y1=﹛x(0 ≤ x ≤ 200);0.7 x+60(x > 200).
(2)由图象可知,交点C的横坐标大于500,
当x﹥500时,设乙商店购物时应付金额为y2元,
则y2=500+0.5(x- 500)=0.5 x+250.
由(1)知,当x﹥500时,y1=0.7 x+60.
由于点C是y1与y2的交点,
∴令0.7 x+60=0.5 x+250.
解得x=950,此时y1=y2=725.
即交点C的坐标为(950,725).
(3)结合图像和(2)可知:
当0 ≤ x ≤ 200或x=950时,
选择甲、乙两家商店购物费用相同;
当200<x<950时,选择甲商店购物更优惠;
当x﹥950时,选择乙商店购物更优惠.
“点睛”本题考查一次函数的应用,方程组等知识,解题是关键是学会构建一次函数,知道利用方程组求两个和尚图象交点坐标,学会利用图象比较函数值大小,属于中考常考题型.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
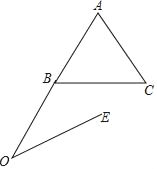
【题目】如图,等边△ABC中,AB=3,点O在AB的延长线上,OA=6,且∠AOE=30°,动点P从点O出发,以每秒![]() 个单位的速度沿射线OE方向运动,以P为圆心,OP为半径作⊙P,同时点Q从点B出发,以每秒1个单位的速度沿折线B…C…A向点A运动,Q与A重合时,P、Q同时停止运动,设P的运动时间为t秒.
个单位的速度沿射线OE方向运动,以P为圆心,OP为半径作⊙P,同时点Q从点B出发,以每秒1个单位的速度沿折线B…C…A向点A运动,Q与A重合时,P、Q同时停止运动,设P的运动时间为t秒.
(1)当△POB是直角三角形时,求t的值;
(2)当⊙P过点C时,求⊙P与线段OA围成的封闭图形的面积;
(3)当⊙P与△ABC的边所在直线相切时,求t的值;
(4)当线段OQ与⊙P只有一个公共点时,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠ACB=90°,AC=8,BC=6,点E是AB中点,将△CAE沿着直线CE翻折,得到△CDE,连接AD,则点E到线段AD的距离等于( )

A.2B.1.8C.1.5D.1.4
查看答案和解析>>
科目:初中数学 来源: 题型:
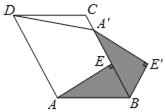
【题目】如图,已知在ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转得到△BA′E′,连接DA′,若∠ADC=60°,AD=5,DC=4,则DA′的大小为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
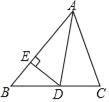
【题目】已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)AB=10,AC=8,DE=3,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边三角形ABC的边长为4 cm,点D从点C出发沿CA向点A运动,点E从点B出发沿AB的延长线BF向右运动,已知点D,E都以每秒![]() cm的速度同时开始运动,运动过程中DE与BC相交于点P.
cm的速度同时开始运动,运动过程中DE与BC相交于点P.

(1).当点D,E运动多少秒后,△ADE为直角三角形?
(2)在点D,E运动时,线段PD与线段PE相等吗?如果相等,予以证明;如不相等,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB和射线BM交于点B.

(1)利用尺规完成以下作图,并保留作图痕迹(不写做法)
①在射线BM上作一点C,使AC=AB,连接AC
②作∠ABM的角平分线交AC于点D
③在射线CM上作一点E,使CE=CD,连接DE
(2)在(1)中所作的图形中,通过观察和测量可以发现BD=DE,请将下面的证明过程补充完整证明:∵AC=AB,
∴∠ =∠
∵BD平分∠ABM,
∴∠DBE=﹣![]() ∠
∠
∵CE=CD
∴∠CDE=∠CED
∴∠ACB=∠CDE+∠CED,
∴∠CED=![]() ∠ACB
∠ACB
∴∠DBE=∠CED,
∴BD=DE,( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com