
【题目】某社区要调查社区居民双休日的体育锻炼情况,采用下列调查方式:
A.从一幢高层住宅楼中选取200名居民;
B.从不同住宅楼中随机选取200居民;
C.选取社区内200名在校学生
(1)上述调查方式最合理的是___________________;
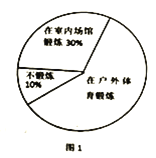
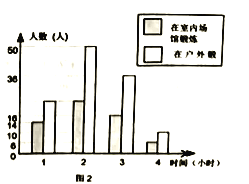
(2)将最合理的调查方式得到的数据制成扇形统计图(如图1)和频数分布直方图(如图2).在这个调查中,200名居民双休日在户外体育锻炼的有_____________人;
(3)调查中的200名居民在户外锻炼1小时的人数为__________________;
(4)请你估计该社区1600名居民双休日体育锻炼时间不少于3小时的人数.
【答案】(1)B (2)120(3)24(4)544人.
【解析】
(1)抽样调查时,为了获得较为准确的调查结果,所以抽样时要注意样本的代表性和广泛性;(2)利用200名居民中,在户外体育锻炼的占60%即可求出答案;(3)在户外体育锻炼的总人数分别减去在户外体育锻炼2小时、3小时、4小时的人数;(4)用样本中学习时间不少于3小时人数占被调查人数比例乘以总人数1600即可.
解:(1)因为抽样调查时,为了获得较为准确的调查结果,所以抽样时要注意样本的代表性和广泛性,所以调查方式最合理的是B;
故答案为:B;
(2)在户外体育锻炼的有200×60%= 120(人),
故答案为:120;
(3)因为在户外体育锻炼2小时、3小时、4小时的人数分别为50、36、10,总人数为120,所以120-50-36-10=24(人),
故答案为:24;
(4)在抽取的200名居民中,双休日体育锻炼时间不少于3小时的有68人
![]() ,
,
所以估计该社区1600名居民双休日体育锻炼时间不少于3小时的人数约为544人.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
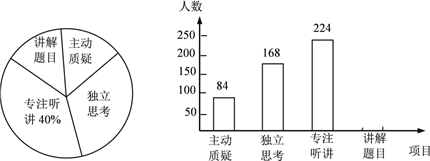
(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初二学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2﹣
x2﹣![]() x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)将△ABC沿x轴翻折后再沿x轴向右平移1个单位,在图中画出平移后的△A1B1C1。
(2)若△ABC内有一点P(a,b),则经过(1)中的两次变换后点P的坐标变为_____________
(3)作出△ABC关于坐标原点O成中心对称的△A2B2C2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都是1,正方形ABCD的四个顶点分别在四条直线上,则正方形ABCD的面积为

A. ![]() B. 5C. 3D.
B. 5C. 3D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).
(1)求证: ![]() ;
;
(2)求△AMN的面积(用a,b,c的代数式表示);
(3)当∠MAN=45°时,求证:c2=2ab.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第1个![]() 中,
中,![]() 40°,
40°,![]() ,在
,在![]() 上取一点
上取一点![]() ,延长
,延长![]() 到
到![]() ,使得在第2个
,使得在第2个![]() 中,
中,![]() ;在
;在![]() 上取一点
上取一点![]() ,延长
,延长![]() 到
到![]() ,使得在第3个
,使得在第3个![]() 中,
中,![]() ;…,按此做法进行下去,第3个三角形中以
;…,按此做法进行下去,第3个三角形中以![]() 为顶点的内角的度数为_____; 第
为顶点的内角的度数为_____; 第![]() 个三角形中以
个三角形中以![]() 为顶点的内角的度数为_____度.
为顶点的内角的度数为_____度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com