Question

2．已知，AB为⊙O的直径，点C为⊙O上一点，过点C作CD⊥AB，垂足为点D，过点C作⊙O的切线交AB的延长线于点E．

（1）如图1，求证：CB平分∠DCE；
（2）如图2，点F在⊙O上，连接OC，∠ECF=2∠OCB，求证：CF=2CD；
（3）如图3，在（2）的条件下，连接AF，若AF=3，CD=3$\sqrt{5}$，求BE的长．

Answer 1

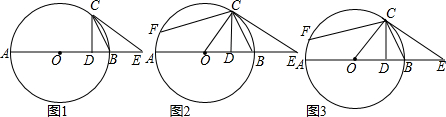
分析 （1）先判断出∠OCB+∠BCE=90°，再判断出∠OCB=∠OBC，即可；
（2）先判断出CF=2CH，然后证明△CHO≌△CDO，最后得到CB平分∠DCE，即可；
（3）先依次判定△CMA≌△CNA，Rt△CMF≌Rt△CNG，再根据勾股定理（2a+3）²-（a+3）²=（6$\sqrt{5}$）²-a²，求出a，最后用（6$\sqrt{5}$-r）²+（3$\sqrt{5}$） ²=r²，求出r．

解答 （1）证明：如图（1），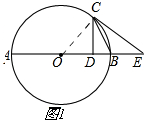

连接OC，
∵CE与⊙O相切，OC是半径，
∴OC⊥CE，
∴∠OCE=90°，
∴∠OCB+∠BCE=90°，
∵CD⊥AB，
∴∠CDB=90°
∴∠DCB+∠DBC=90°，
∵OC=OB，
∴∠OCB=∠OBC
∴∠DCB=∠BCE，
∴CB平分∠DCE，
（2）证明：如图（2），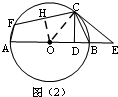

过O作OH⊥CF于H，
∵OH过圆心，
∴CF=2CH
由（1）可知：CB平分∠DCE，
∴∠DCE=2∠DCB，
∵∠ECF=2∠OCB，
∴∠FCD=2∠OCD，
∴∠FCO=∠OCD，
∵∠CDO=∠CHO=90° OC=OC，
∴△CHO≌△CDO
∴CH=CD，
∴CF=2CD，
（3）如图（3），

延长CD交⊙O于G，分别连接AG、AC，过C作CM⊥AF于M，过C作CN⊥AG于N．
∵CD⊥AB  AB是直径，
∴CG=2CD     
由（2）可知CF=2CD，
∴CG=CF
∴∠CAG=∠CAF；
∴AC平分∠FAG
∵M⊥AF  CN⊥AG，
∴CM=CN，∠CMA=∠CNA=90°
∴△CMA≌△CNA，
∴AM=AN，
∵CM=CN  CF=CG，
∴Rt△CMF≌Rt△CNG，
∴MF=NG，
设MF=a  则NG=a，
∵AF=3，
∴MA=a+3，
∴AN=a+3，
∴AG=2a+3，
∵CD⊥AB CD=GD
∴AD垂直平分CG，
∴CA=GA=2a+3
在Rt△CMA中，CM²=CA²-AM²=（2a+3）²-（a+3）²
在Rt△CMF中，CM²=CF²-MF²=（6$\sqrt{5}$）²-a²
∴（2a+3）²-（a+3）²=（6$\sqrt{5}$）²-a²  
∴a₁=-$\frac{15}{2}$ （舍），a₂=6
∴AM=9，AC=AG=15，
∴AD=$\sqrt{1{5}^{2}-（3\sqrt{5}）^{2}}$=6$\sqrt{5}$
设⊙O的半径为r，在Rt△CDO中，（6$\sqrt{5}$-r）²+（3$\sqrt{5}$） ²=r²，
∴r=$\frac{15\sqrt{5}}{4}$，
∴OD=$\frac{9\sqrt{5}}{4}$，
∴cos∠COD=$\frac{OD}{OC}$=$\frac{3}{5}$，
在Rt△COE中cos∠COD=$\frac{OC}{OE}$=$\frac{3}{5}$，
∴OE=$\frac{25\sqrt{5}}{4}$，
∴BE=$\frac{5\sqrt{5}}{2}$．

点评 此题是圆的综合题，主要考查了勾股定理，全等三角形的判定和性质，角平分线的性质，锐角三角函数，解本题的关键是用判定三角形全等．