
【题目】甲、乙两车从A地将一批物品匀速运往B地,已知甲出发0.5h后乙开始出发,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,请结合图中的信息解决如下问题: 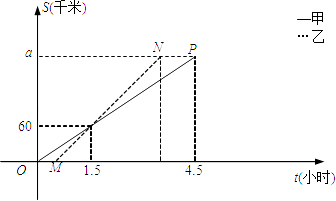
(1)计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回. ①在图中画出乙车在返回过程中离A地的距离S(km)与时间t(h)的函数图象;
②请问甲车在离B地多远处与返程中的乙车相遇?
【答案】
(1)解:由题意可知M(0.5,0),线段OP、MN都经过(1.5,60),
甲车的速度60÷1.5=40km/小时,
乙车的速度60÷(1.5﹣0.5)=60km/小时,
a=40×4.5=180km;
(2)解:①∵180÷60=3小时,
∴乙车到达B地,所用时间为180÷60=3,所以点N的横坐标为3.5,
6.5小时返回A地,
乙车在返回过程中离A地的距离S(km)与时间t(h)的函数图象为线段NQ;

②甲车离A地的距离是:40×3.5=140km;
设乙车返回与甲车相遇所用时间为t0,
则(60+40)t0=180﹣140,
解得t0=0.4h,
60×0.4=24km,
答:甲车在离B地24km处与返程中的乙车相遇.
【解析】(1)表示出M点的坐标,再根据速度=路程÷时间,分别列式进行计算即可求出两车的速度,再根据甲到达的时间为4.5小时,然后利用路程=速度×时间列式计算即可求出a的值;(2)①求出甲走完全程的时间,从而得到返回A地的时间,然后作出图形即可;②先根据相遇问题求出甲车返回途中与乙车相遇的时间,再根据路程=速度×时间求解即可.


科目:初中数学 来源: 题型:
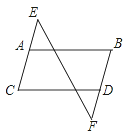
【题目】如图,有以下3句话:①AB∥CD,②∠B=∠C、③∠E=∠F、请以其中2句话为条件,第三句话为结论构造命题.
(1)你构造的是哪几个命题?
(2)你构造的命题是真命题还是假命题?请加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决问题时需要思考:是否解决过与其类似的问题.小明从问题1解题思路中获得启发从而解决了问题2.
(1)问题1:如图①,在正方形ABCD中,E、F是BC、CD上两点,∠EAF=45°. 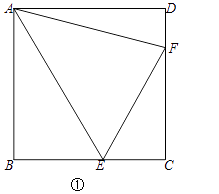
求证:∠AEF=∠AEB.
小明给出的思路为:延长EB到H,满足BH=DF,连接AH.请完善小明的证明过程.
(2)问题2:如图②,在等腰直角△ABC中,∠ACB=90°,AC=BC=4,D为AB中点,E、F是AC、BC边上两点,∠EDF=45°. 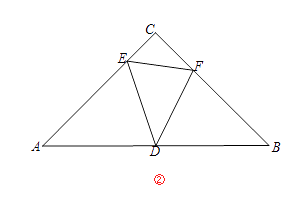
①求点D到EF的距离.
②若AE=a,则S△DEF=(用含字母a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生课外阅读的喜好,某校从八年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其它”类统计。图(1)与图(2)是整理数据后绘制的两幅不完整的统计图。以下结论不正确的是( )
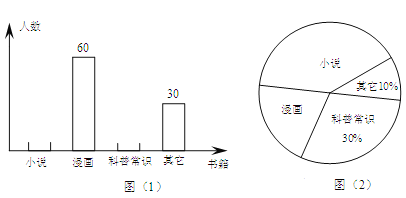
A. 由这两个统计图可知喜欢“科普常识”的学生有90人.
B. 若该年级共有1200名学生,则由这两个统计图可估计喜爱“科普常识”的学生约有360个.
C. 由这两个统计图不能确定喜欢“小说”的人数.
D. 在扇形统计图中,“漫画”所在扇形的圆心角为72°.
查看答案和解析>>
科目:初中数学 来源: 题型:
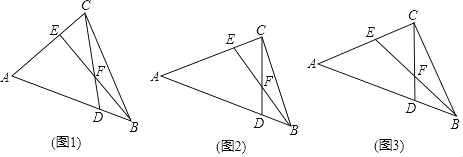
【题目】如图,在△ABC中,点D在边AB上,点E在边AC上,CE=BD,连接CD,BE,BE与CD相交于点F.
(1)如图1,若△ACD为等边三角形,且CE=DF,求∠CEF的度数;
(2)如图2,若AC=AD,求证:EF=FB;
(3)如图3,在(2)的条件下,若∠CFE=45°,△BCD的面积为4,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:同弧或等弧所对的圆周角相等.也就是,如图(1),⊙O中, ![]() 所对的圆周角∠ACB=∠ADB=∠AEB.
所对的圆周角∠ACB=∠ADB=∠AEB. 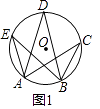
(1)已知:如图(2),矩形ABCD. 
①若AB< ![]() BC,在边AD上求作点P,使∠BPC=90°.(保留作图痕迹,写出作法.)
BC,在边AD上求作点P,使∠BPC=90°.(保留作图痕迹,写出作法.)
②小明经研究发现,当AB、BC的大小关系发生变化时,①中点P的个数也会发生变化,请你就点P的个数,探讨AB与BC之间的数量关系.(直接写出结论)
创新
(2)小明经进一步研究发现:命题“若四边形的一组对边相等和一组对角相等,则这个四边形是平行四边形.”是一个假命题,并在平行四边形的基础上利用“同弧或等弧所对的圆周角相等.”作出了一个反例图形.请你利用下面如图(3)所给的□ABCD作出该反例图形.(不写作法,保留作图痕迹) 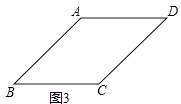
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,O为AC中点,EF过点O且EF⊥AC分别交DC于点F,交AB于点E,点G是AE中点且∠AOG=30°,给出以下结论: ①∠AFC=120°;
②△AEF是等边三角形;
③AC=3OG;
④S△AOG= ![]() S△ABC
S△ABC
其中正确的是 . (把所有正确结论的序号都选上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是 .
.其中正确结论的序号是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com