
����Ŀ�����������������й���ͳ��ѧ����Ҫ���������춨���й���ͳ��ѧ�Ļ�����ܣ����Ĵ����ɾ���Ҫ�������������������ͷ����������У��������ǡ�������������ߵ���ѧ�ɾͣ�
�������������м��أ��������˹����˳��ţ�ӯʮһ���˳���������ʮ���������������۸������Σ�
���ģ������м����˹�ͬ��Ǯ�����ÿ�˳���Ǯ����ô����ʮһǮ�����ÿ�˳���Ǯ����ô����ʮ��Ǯ���ʣ��м����˹�ͬ��Ǯ�����ļ�Ǯ�Ƕ��٣���
����x���˹�ͬ�����ļ�Ǯ��yǮ������������з�����Ϊ__________��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB��90������BOC��30����OMƽ�֡�AOC��ONƽ�֡�BOC��

��1�����MON�Ķ�����
��2������BOC��60���������������䣬���MON���� ����
��3������AOB�����������������䣬���MON�Ķ�����
��4��������Ľ���ܿ���ʲô���ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����Rt��ABC�У���C=90�㣬AC=6��BC=8������P�ӵ�A��ʼ�ر�AC���C��1����λ���ȵ��ٶ��˶�������Q�ӵ�C��ʼ�ر�CB���B��ÿ��2����λ���ȵ��ٶ��˶�������P��PD��BC����AB�ڵ�D������PQ�ֱ�ӵ�A��Cͬʱ������������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����
��1��ֱ���ú�t�Ĵ���ʽ�ֱ��ʾ��QB=�� ����PD=�� ����
��2���Ƿ����t��ֵ��ʹ�ı���PDBQΪ���Σ������ڣ����t��ֵ���������ڣ�˵�����ɣ���̽����θı�Q���ٶȣ������˶�����ʹ�ı���PDBQ��ijһʱ��Ϊ���Σ����Q���ٶȣ�
��3����ͼ2���������˶������У�����߶�PQ�е�M��������·������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���ABCD�����Σ�AB=4����ABC=60������EAF�����߷ֱ�������CB��DC�ཻ�ڵ�E��F������EAF=60����

��1����ͼ1������E���߶�CB���е�ʱ��ֱ��д���߶�AE��EF��AF֮���������ϵ��
��2����ͼ2������E���߶�CB������һ��ʱ����E����B��C�غ�������֤��BE=CF��
��3����ͼ3������E���߶�CB���ӳ����ϣ�����EAB=15��ʱ�����F��BC�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�У��Խ���BD���ڵ�ֱ����������E��F����BE=DF������AE��AF��CE��CF����ͼ��ʾ��
��1����֤����ABE�ա�ADF��
��2�����ж��ı���AECF����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A(n��-2)��B(1��4)��һ�κ���y=kx+b��ͼ��ͷ���������y=![]() ��ͼ����������㣬ֱ��AB��y�ύ�ڵ�C��
��ͼ����������㣬ֱ��AB��y�ύ�ڵ�C��
(1)����������һ�κ����Ĺ�ϵʽ��
(2)����AOC�������
(3)��ʽkx+b-![]() <0�Ľ⼯(ֱ��д����)��
<0�Ľ⼯(ֱ��д����)��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ɸ���ȫ��ͬ��С��������ɵ�һ�������壮
��1��������ʵ��������������˳�λ�����������������ͼ������ͼ����ͼ��

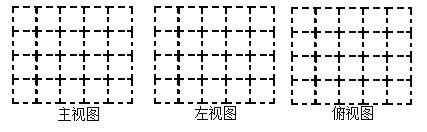
��2�������������������õ�һЩС�����壬��������������������ͼ����ͼ���䣬��ô�������õ�___________С�����壻
��3������������������������һЩ��ͬ��С�����壬��������������������ͼ����ͼ���䣬��ô������������________��С�����壮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ƽ��ֱ������ϵxOy�У�������y=ax2��2x+c��x�ύ�ڵ�A�͵�B��1��0������y���ཻ�ڵ�C��0��3����
��1���������ߵĽ���ʽ�Ͷ���D�����ꣻ
��2����֤����DAB=��ACB��
��3����Q���������ϣ�����ADQ����ADΪ�ĵ��������Σ���Q������꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y=mx2��2mx+n��m��0���Ķ���ΪA����x�ύ��B��C���㣨��B�ڵ�C��ࣩ����y�������ύ�ڵ�D������AD���ӳ���x����E����AC��DC��S��DEC��S��AEC=3��4��
��1�����E�����ꣻ
��2����AEC�ܷ�Ϊֱ�������Σ����ܣ������ʱ�����ߵĺ�������ʽ�������ܣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com