
【题目】如图1,已知点A(-2,0).点D在y轴上,连接AD并将它沿x轴向右平移至BC的位置,且点B坐标为(4,0),连接CD,OD=![]() AB.
AB.
(1)线段CD的长为 ,点C的坐标为 ;
(2)如图2,若点M从点B出发,以1个单位长度/秒的速度沿着x轴向左运动,同时点N从原点O出发,以相同的速度沿折线OD→DC运动(当N到达点C时,两点均停止运动).假设运动时间为t秒.
①t为何值时,MN∥y轴;
②求t为何值时,S△BCM=2S△ADN.

【答案】(1)6,(6,3);(2)①![]() ;②
;②![]() 为
为![]() 或6.
或6.
【解析】
(1)由平移的性质可得四边形ABCD是平行四边形,可得AB=CD=6,由题意可求点C坐标;
(2)由题意列出方程,可求解;
(3)分两种情况讨论,列出方程可求解.
(1)∵点A(-2,0),点B坐标为(4,0),
∴AB=6
∵将AD沿x轴向右平移至BC的位置,
∴AD∥BC,AD=BC
∴四边形ABCD是平行四边形
∴CD=AB=6,CD∥AB
∵OD=![]() AB.
AB.
∴OD=3,且CD∥AB
∴点C(6,3)
故答案为:6,(6,3);
(2)∵MN∥y轴,
∴点N在CD上,
∴4-t=t-3
∴t=![]()
∴当t=![]() s时,MN∥y轴;
s时,MN∥y轴;
(3)当点N在OD上时,
∵S△BCM=2S△ADN.
∴![]() ×3×t=2×
×3×t=2×![]() ×2×(3-t)
×2×(3-t)
解得:t=![]()
当点N在CD上时,
∵S△BCM=2S△ADN.
∴![]() ×3×t=2×
×3×t=2×![]() ×3×(t-3)
×3×(t-3)
解得:t=6
综上所述:t=6或![]() 时,S△BCM=2S△ADN.
时,S△BCM=2S△ADN.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】已知等边三角形![]() 的高为6,在这个三角形所在的平面内有一个点
的高为6,在这个三角形所在的平面内有一个点![]() ,若点
,若点![]() 到
到![]() 的距离是1,点
的距离是1,点![]() 到
到![]() 的距离是2,则点
的距离是2,则点![]() 到
到![]() 的最小距离与最大距离分别是_______.
的最小距离与最大距离分别是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图①,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(![]() ,0),B(3,0),与y轴交于点C,连接BC.
,0),B(3,0),与y轴交于点C,连接BC.
(1)求抛物线的表达式;
(2)抛物线上是否存在点M,使得△MBC的面积与△OBC的面积相等,若存在,请直接写出点M的坐标;若不存在,请说明理由;
(3)点D(2,m)在第一象限的抛物线上,连接BD.在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校提倡练字,小冬和小红一起去文具店买钢笔和字帖,小冬在文具店买1支钢笔和3本字帖共花了38元,小红买了2支钢笔和4本字帖共花了64元.
(1)每支钢笔与每本字帖分别多少元?
(2)帅帅在六一节当天去买,正巧碰到文具店搞促销,促销方案有两种形式:
①所购商品均打九折
②买一支钢笔赠送一本字帖
帅帅要买5支钢笔和15本字帖,他有三种选择方案:
(Ⅰ)一次买5支钢笔和15本字帖,然后按九折付费;
(Ⅱ)一次买5支钢笔和10本字帖,文具店再赠送5本字帖;
(Ⅲ)分两次购买,第一次买5支钢笔,文具店会赠送5本字帖,第二次再去买10本字帖,可以按九折付费;问帅帅最少要付多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
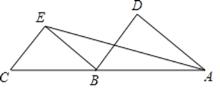
【题目】已知A,B,C三点在同一直线上,∠DAE=∠AEB,∠D=∠BEC,
(1)求证:BD∥CE;
(2)若∠C=70°,∠DAC=50°,求∠DBE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
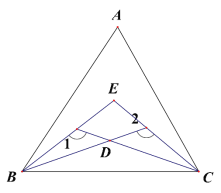
【题目】(1)如图,△ABC, ∠ABC、∠ACB 的三等分线交于点 E、D, 若∠1=130°,∠2=110°,求∠A 的度数。
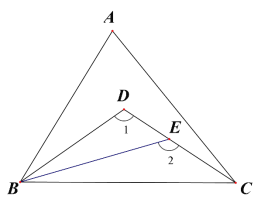
(2)如图,△ABC,∠ABC 的三等分线分别与∠ACB 的平分线交于点 D,E 若∠1=110°,∠2=130°,求∠A 的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形中,顶角等于36°的等腰三角形称为黄金三角形,如图,△ABC中,AB=AC,且∠A=36°.

(1)在图中用尺规作边AB的垂直平分线交AC于D,连接BD(保留作图痕迹,不写作法).
(2)请问△BDC是不是黄金三角形,如果是,请给出证明,如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
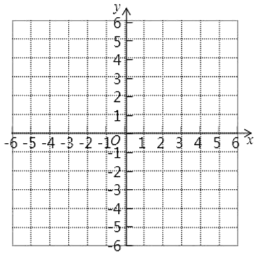
(1)先作出△ABC,再将△ABC向下平移5个单位长度后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得得到△A2B2C2,请画出△A2B2C2;
(3)求出以O,A1,B为顶点的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知a,b,c均为实数,且![]() +|b+1|+(c+2)2=0,求关于x的方程ax2+bx+c=0的根;
+|b+1|+(c+2)2=0,求关于x的方程ax2+bx+c=0的根;
(2)已知二次函数y=ax2+bx+c的图象经过A(﹣1,0),B(0,﹣3),C(4,5)三点,求该二次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com