
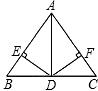
 如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E,F,BD=DC,求证:AD⊥BC.
如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E,F,BD=DC,求证:AD⊥BC.  期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{a+b}$÷(a+b)=1 | B. | 2ab•$\frac{3{b}^{2}}{2a}$=3b2 | ||
| C. | $\frac{{a}^{2}-9}{a}$÷$\frac{{a}^{2}+3a}{{a}^{2}}$=a-3 | D. | $\frac{{x}^{2}+8x+16}{x-4}$$•\frac{1}{x+4}$=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
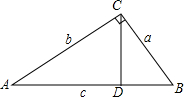 如图,△ABC中,∠ACB=90°,AB=c,BC=a,AC=b,且(c-$\sqrt{8}$)2+|$\sqrt{2}$-a|=0.
如图,△ABC中,∠ACB=90°,AB=c,BC=a,AC=b,且(c-$\sqrt{8}$)2+|$\sqrt{2}$-a|=0.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
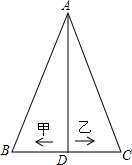 如图是三角形的土地ABC,AB=AC,△ABC中间一条小路AD,AD平分∠BAC,交BC于点D.甲、乙两人从点D出发,分别步行到B、C两点,则甲、乙两人步行的距离( )
如图是三角形的土地ABC,AB=AC,△ABC中间一条小路AD,AD平分∠BAC,交BC于点D.甲、乙两人从点D出发,分别步行到B、C两点,则甲、乙两人步行的距离( )| A. | 甲步行的路程远 | B. | 乙步行的路程远 | C. | 一样远 | D. | 无法比较 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com