
【题目】如图,菱形ABCD的周长为16,若![]() ,E是AB的中点,则点E的坐标为_____________.
,E是AB的中点,则点E的坐标为_____________.

【答案】![]()
【解析】首先求出AB的长,进而得出EO的长,再利用锐角三角函数关系求出E点横纵坐标即可.
解:如图所示,过E作EM⊥AC,
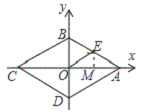
已知四边形ABCD是菱形,且周长为16,∠BAD=60°,根据菱形的性质可得AB=CD-BC=AD=4,AC⊥DB,∠BAO=![]() ∠BAD=30°,又因E是AB的中点,根据直角三角形中,斜边的中线等于斜边的一半可得EO=EA=EB=
∠BAD=30°,又因E是AB的中点,根据直角三角形中,斜边的中线等于斜边的一半可得EO=EA=EB=![]() AB=2,根据等腰三角形的性质可得∠BAO=∠EOA=30°,由直角三角形中,30°的锐角所对的直角边等于斜边的一半可得EM=
AB=2,根据等腰三角形的性质可得∠BAO=∠EOA=30°,由直角三角形中,30°的锐角所对的直角边等于斜边的一半可得EM=![]() OE=1,在Rt△OME中,由勾股定理可得OM=
OE=1,在Rt△OME中,由勾股定理可得OM=![]() ,所以点E的坐标为(
,所以点E的坐标为(![]() ,1),
,1),
故选B.
“点睛”此题主要考查了菱形的性质以及锐角三角函数关系应用,根据已知得出EO的长以及∠EOA=∠EAO=30°是解题的关键.


科目:初中数学 来源: 题型:
【题目】黄桃是我县南楼乡东里双村的一大特产,现有20筐黄桃,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值 (单位:千克) |
|
|
| 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐黄桃中,与标准质量差值为![]() 千克的有________筐,最重的一筐重________千克,最轻的一筐重________千克,最重的一筐比最轻的一筐重________千克;
千克的有________筐,最重的一筐重________千克,最轻的一筐重________千克,最重的一筐比最轻的一筐重________千克;
(2)与标准重量比较,20筐黄桃总计超过多少千克?
(3)若黄桃每千克售价3元,则出售这20筐黄桃可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
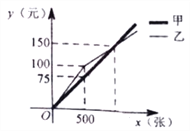
【题目】某社区准备进行“为了地球,远离白色污染”的宣传活动,需要制定宣传单,选择社区附近的甲、乙两家印刷社印刷,他们各自制作这种宣传单的费用y(元)与宣传单数量x(张)之间的函数图象如图所示,结合图象解答下列问题:
(1)求甲印刷社制作这种宣传单每张的钱数.
(2)当x>500时,求乙印刷社所需的费用y与x之间的函数关系式.
(3)如果该社区在制作这种宣传单时,第一次印刷了800张宣传单,第二次印刷了1200张宣传单,直接写出该社区两次印刷这种宣传单共花费的最少钱数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】育红学校七年级学生步行到郊外旅行.七(1)班的学生组成前队,步行速度为4km/h,七(2)班的学生组成后队,速度为6km/h.前队出发1h后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12km/h.
(1)当联络员追上前队时,离出发点多远?
(2)当联络员追上前队再到后队集合,总共用了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E在BC边上,AF平分∠DAE,DF//AE,AF与CD相交于点G.
(1)如图1,当∠AEC =![]() ,AE=4时,求FG的长;
,AE=4时,求FG的长;
(2)如图2,在AB边上截取点H,使得DH=AE,DH与AF、AE分别交于点M、N,求证:AE=AH+DG

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片ABCD中,EF∥AB,M,N是线段EF的两个动点,且MN=![]() EF,若把该正方形纸片卷成一个圆柱,使点A与点B重合,若底面圆的直径为6cm,则正方形纸片上M,N两点间的距离是____________cm.
EF,若把该正方形纸片卷成一个圆柱,使点A与点B重合,若底面圆的直径为6cm,则正方形纸片上M,N两点间的距离是____________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某校全校学生从学校步行去烈士陵园扫墓,他们排成长为250米的队伍,以50米/分钟的平均速度行进,当排头出发20分钟后,学校有一份文件要送给带队领导,一名教师骑自行车以150米/分钟的平均速度按原路追赶学生队伍,学校离烈士陵园2千米.
(1)教师能否在排头队伍到达烈士陵园前送到在排头前带队领导手里?
(2)送信教师和带队领导停下来交谈了一分钟,交谈过程中队伍继续前进,然后领导要求送信老师马上赶到队尾,防止有意外情况发生,他按追赶时的平均速度需要多少时间就可以赶到队尾;
(3)送信教师赶到队尾后,和最后的同学一起走,送信老师还需要多少时间可到达烈士陵园.
查看答案和解析>>
科目:初中数学 来源: 题型:
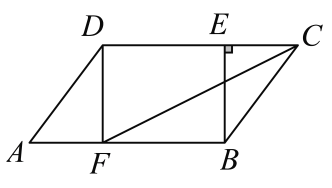
【题目】在![]() ABCD中,过点B作BE⊥CD于点E,点F在边AB上,AF=CE,连接DF,CF.
ABCD中,过点B作BE⊥CD于点E,点F在边AB上,AF=CE,连接DF,CF.
(1)求证:四边形DFBE是矩形;
(2)当CF平分∠DCB时,若CE=3,BE=4,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com