
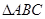 的三边,试说明
的三边,试说明 .(本题6分)
.(本题6分)科目:初中数学 来源:不详 题型:解答题
 吨, 则粗加工的吨数为 吨,加工这批海产品需要 天, 可获利 元(用含
吨, 则粗加工的吨数为 吨,加工这批海产品需要 天, 可获利 元(用含 的代数式表示);
的代数式表示); 在什么范围内时, 该企业加工这批海产品的获利不低于120000元?
在什么范围内时, 该企业加工这批海产品的获利不低于120000元?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com