
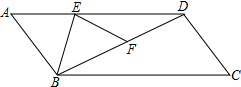
 E为?ABCD边AD上一点,将△ABE沿BE翻折得到△FBE,点F在BD上,且EF=DF.若∠C=52°,那么∠ABE=51°.
E为?ABCD边AD上一点,将△ABE沿BE翻折得到△FBE,点F在BD上,且EF=DF.若∠C=52°,那么∠ABE=51°. 分析 由平行四边形的性质和折叠的性质得出∠BFE=∠A=52°,∠FBE=∠ABE,由等腰三角形的性质和三角形的外角性质得出∠EDF=∠DEF=$\frac{1}{2}$∠BFE=26°,由三角形内角和定理求出∠ABD=102°,即可得出∠ABE的度数.
解答 解:∵四边形ABCD是平行四边形,
∴∠A=∠C=52°,
由折叠的性质得:∠BFE=∠A=52°,∠FBE=∠ABE,
∵EF=DF,
∴∠EDF=∠DEF=$\frac{1}{2}$∠BFE=26°,
∴∠ABD=180°-∠A-∠EDF=102°,
∴∠ABE=$\frac{1}{2}$∠ABD=51°;
故答案为:51°.
点评 本题考查了平行四边形的性质、折叠的性质、等腰三角形的性质、三角形的外角性质、三角形内角和定理;熟练掌握平行四边形的性质和等腰三角形的性质是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 扩大为原来的2倍 | B. | 缩小为原来的$\frac{1}{2}$ | C. | 不变 | D. | 缩小为原来的$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2xy+6xz+3=2x(y+3z)+3 | B. | (x+6)(x-6)=x2-36 | ||
| C. | -2x2-2xy=-2x(x+y) | D. | 3a2-3b2=3(a2-b2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了了解某中学初中二年级150名男学生的身体发育情况,从中对20名男学生的身高进行了测量,结果如下:(单位:厘米)
为了了解某中学初中二年级150名男学生的身体发育情况,从中对20名男学生的身高进行了测量,结果如下:(单位:厘米)| 分组 | 频数 | 频率 |
| 156.5~161.5 | 3 | 0.15 |
| 161.5~166.5 | 2 | 0.10 |
| 166.5~171.5 | 4 | |
| 171.5~176.5 | 0.30 | |
| 176.5~181.5 | ||
| 合计 | 20 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,菱形ABCD的边长为4,∠ABC=120°.点E是AB边上的动点,点F是对角线AC上的动点,则EF+BF的最小值为2$\sqrt{3}$.
如图,菱形ABCD的边长为4,∠ABC=120°.点E是AB边上的动点,点F是对角线AC上的动点,则EF+BF的最小值为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在正方形网格中,每个小正方形的顶点称为格点,过格点E在四边形ABCD内作矩形EFGH,使得F、G、H分别落在边BC、CD、DA上.
在正方形网格中,每个小正方形的顶点称为格点,过格点E在四边形ABCD内作矩形EFGH,使得F、G、H分别落在边BC、CD、DA上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,折叠矩形纸片ABCD,使点D落在边AB上,折痕EF的两端分别在CD、AD上(含端点),且AB=10cm,BC=6cm,当折痕EF最长时DF=$\frac{10}{3}$cm.
如图,折叠矩形纸片ABCD,使点D落在边AB上,折痕EF的两端分别在CD、AD上(含端点),且AB=10cm,BC=6cm,当折痕EF最长时DF=$\frac{10}{3}$cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com