
 如图,在平面直角坐标系中,正方形OBCD的点B的坐标为(2,0),E,F分别为边BC,CD上的点,且BE=CF,连结OE,BF,交点为G,将△BCF沿BF对折,得到△BPF,延长FP交x轴于点Q.
如图,在平面直角坐标系中,正方形OBCD的点B的坐标为(2,0),E,F分别为边BC,CD上的点,且BE=CF,连结OE,BF,交点为G,将△BCF沿BF对折,得到△BPF,延长FP交x轴于点Q.分析 (1)根据全等三角形的判定方法,判断出△BEO≌△CFB,即可判断出∠BEO=∠CFB,然后根据∠CFB+∠CBF=90°,可得∠BEO+∠CBF=90°,所以∠EGB=90°,所以OE⊥BF,据此判断即可;
(2)首先根据对折的性质,可得BP⊥FP,CP⊥BF,据此求出点P的坐标是多少,进而根据点F的坐标,确定出FP所在的直线的解析式;然后求出FP所在的直线与x轴的交点坐标是多少,即可求出点Q的坐标.
(3)首先根据点E的坐标为(2,n),BE=CF,求出点F的坐标是多少;然后确定出FQ所在的直线的解析式,进而求出点P的坐标是多少;最后根据DF∥QO,可得$\frac{DF}{QO}=\frac{DP}{OP}$,据此写出关于n的函数关系式即可.
解答 解:(1)在△BEO和△CFB中,
$\left\{\begin{array}{l}{BE=CF}\\{∠EBO=∠FCB}\\{BO=CB}\end{array}\right.$
∴△BEO≌△CFB,
∴∠BEO=∠CFB,
∵∠CFB+∠CBF=90°,
∴∠BEO+∠CBF=90°,
∴∠EGB=180°-90°=90°,
∴OE⊥BF.
(2)设点P的坐标是(a,b),
∵E为BC的中点,BE=CF,
∴F为CD的中点,
∴C(2,2),F(1,2),
∵BP⊥FP,
∴$\frac{b-0}{a-2}×\frac{b-2}{a-1}=-1$,
整理,可得
(a-1)(a-2)+b(b-2)=0…①;
∵CP⊥BF,
∴$\frac{b-2}{a-2}×\frac{2-0}{1-2}=-1$,
整理,可得
a=2b-2…②;
把②代入①,可得
b=$\frac{6}{5}$,或b=2(舍去),
∴a=2×$\frac{6}{5}-2$=$\frac{2}{5}$,
∴点P的坐标是($\frac{2}{5},\frac{6}{5}$),
∴FP所在的直线的解析式是:
$\frac{x-1}{x-\frac{2}{5}}=\frac{y-2}{y-\frac{6}{5}}$,
令y=0,可得
$\frac{x-1}{x-\frac{2}{5}}=\frac{-2}{-\frac{6}{5}}$,
解得x=-$\frac{1}{2}$,
∴点Q的坐标是(-$\frac{1}{2}$,0).
(3)∵点E的坐标为(2,n),BE=CF,
∴点F的坐标是(2-n,2),
∴FQ所在的直线的解析式是:
$\frac{x-2}{x+m}=\frac{y-n}{y}$,
令x=0,解得y=$\frac{mn}{m+2}$,
∴点P的坐标是(0,$\frac{mn}{m+2}$),
∵DF∥QO,
∴$\frac{DF}{QO}=\frac{DP}{OP}$,
∴$\frac{2-n}{m}=\frac{2-\frac{mn}{m+2}}{\frac{mn}{m+2}}$,
整理,可得
n2-(m+2)n+2m+4=0.
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了全等三角形的判定和性质的应用,要熟练掌握全等三角形的判定方法.
(3)此题还考查了点的坐标的求法,以及直线的解析式的求法,还有两条直线相互垂直的性质的应用,要熟练掌握.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
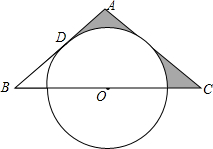 在△ABC中,AB=AC,O是BC中点,BC=12$\sqrt{3}$cm,AB与⊙O相切于点D,AD:DB=1:3
在△ABC中,AB=AC,O是BC中点,BC=12$\sqrt{3}$cm,AB与⊙O相切于点D,AD:DB=1:3查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,AB是⊙O的直径,BC切⊙O于B,AC交⊙O于P,D为BC边的中点,连接DP.
已知:如图,AB是⊙O的直径,BC切⊙O于B,AC交⊙O于P,D为BC边的中点,连接DP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
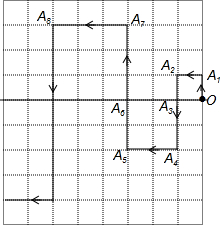 在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向左、向下、向左的方向依次不断移动得A1,A2,A3,A4,A5,…,每次移动的距离分别为1,1,1,2,2,2,3,3,3…,其行走路线如图所示:
在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向左、向下、向左的方向依次不断移动得A1,A2,A3,A4,A5,…,每次移动的距离分别为1,1,1,2,2,2,3,3,3…,其行走路线如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将矩形纸片的两只直角分别沿EF、DF翻折,点B恰好落在AD边上的点B′处,点C恰好落在边B′F上.若AE=3,BE=5,则FC=4.
如图,将矩形纸片的两只直角分别沿EF、DF翻折,点B恰好落在AD边上的点B′处,点C恰好落在边B′F上.若AE=3,BE=5,则FC=4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
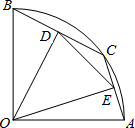 如图,在半径为4的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E.若四边形AOBC的面积为10,则△DOE的面积是$\frac{9}{2}$.
如图,在半径为4的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E.若四边形AOBC的面积为10,则△DOE的面积是$\frac{9}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com