
【题目】顺次连接等腰梯形各边中点所成的四边形是
【答案】菱形
【解析】解:已知:等腰梯形ABCD中,AD∥BC,AB=CD,E、F、G、H分别是各边的中点, 求证:四边形EFGH是菱形
证明:连接AC、BD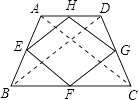
∵E、F分别是AB、BC的中点
∴EF= ![]() AC
AC
同理FG= ![]() BD,GH=
BD,GH= ![]() AC,EH=
AC,EH= ![]() BD
BD
又∵四边形ABCD是等腰梯形
∴AC=BD
∴EF=FG=GH=HE
∴四边形EFGH是菱形.
所以答案是:菱形.
【考点精析】认真审题,首先需要了解三角形中位线定理(连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半),还要掌握菱形的判定方法(任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形)的相关知识才是答题的关键.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】适合下列条件的△ABC中,直角三角形的个数为( ) ①a=3,b=4,c=5;
②a=6,∠A=45°;
③a=2,b=2,c=2 ![]() ;
;
④∠A=38°,∠B=52°.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,动点P从点A出发,以1cm/s的速度向点D运动;动点Q从点C同时出发,以3cm/s的速度向点B运动.规定当其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t,求: 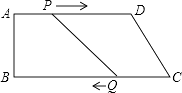
(1)当t为何值时,PQ∥CD?
(2)当t为何值时,PQ=CD?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列生活现象中,不是平移现象的是 ( )
A. 小亮荡秋千的运动B. 左右推动的推拉窗帘
C. 站在运行的电梯上的人D. 坐在直线行驶的列车上的乘客
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中注有“今两算得失相反,要令正负以名之.”意思是:“今有两数若其意义相反,则分别叫做正数和负数.”规定向东为正,向西为负.若向东走70m,记作+70m,则﹣20m表示( )
A.向西走20mB.向东走20mC.向西走50mD.向东走50m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将直角三角形ABC沿斜边AC的方向平移到三角形DEF的位置,DE交BC于点G,BG=4,EF=12,三角形BEG的面积为4,下列结论:①DE⊥BC;②三角形ABC平移的距离是4;③AD=CF;④四边形GCFE的面积为20,其中正确的结论有( )
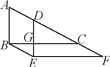
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及S四边形ABDC.
(2)在y轴上是否存在一点Q,连接QA,QB,使S△QAB=S四边形ABDC?若存在这样一点,求出点Q的坐标;若不存在,试说明理由.
(3)如图②,点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合),给出下列结论:①![]() 的值不变,②
的值不变,②![]() 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com