
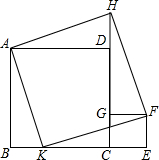
 已知,如图,四边形ABCD和CEFG都是正方形,点K在BC上,延长CD到点H,使DH=CE=BK.求证:四边形AKFH是正方形.
已知,如图,四边形ABCD和CEFG都是正方形,点K在BC上,延长CD到点H,使DH=CE=BK.求证:四边形AKFH是正方形. 证明:∵四边形ABCD和CEFG都是正方形,
证明:∵四边形ABCD和CEFG都是正方形,
|


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源: 题型:
| A、32.06×1012元 |
| B、3.206×1011元 |
| C、3.206×1010元 |
| D、3.206×1012元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
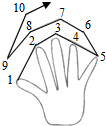 请同学们伸出左手,一起做下面的游戏:从大拇指开始,依次数数字1、2、3、4、5,然后从无名指开始倒着数6、7、8、9,再从食指开始数10、11、12、13,…请问数字20落在哪个手指上?200?2000呢?
请同学们伸出左手,一起做下面的游戏:从大拇指开始,依次数数字1、2、3、4、5,然后从无名指开始倒着数6、7、8、9,再从食指开始数10、11、12、13,…请问数字20落在哪个手指上?200?2000呢?查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值.
(1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值. |
| AC |
 |
| CB |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
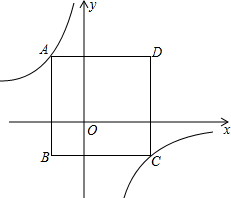 如图,边长为6的正方形ABCD置于平面直角坐标系xOy中,且AB平行于y轴,已知点A的横坐标为-2,反比例函数y=
如图,边长为6的正方形ABCD置于平面直角坐标系xOy中,且AB平行于y轴,已知点A的横坐标为-2,反比例函数y=| k |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com