
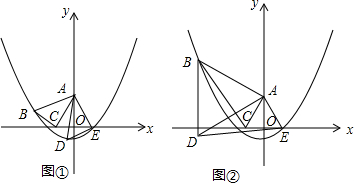
·ЦОц ЈЁ1Ј©УЙРэЧӘөДРФЦКҝЙЦӘЈ»AC=AEЈ¬ЎПCAE=60ЎгЈ¬ТАҫЭөИСьИэҪЗРОИэПЯәПТ»өДРФЦКҝЙЦӘOC=OEЈ¬ЎПCAO=30ЎгЈ¬ТАҫЭМШКвИсҪЗИэҪЗәҜКэЦөҝЙЗуөГOCөДіӨЈ¬ҙУ¶шөГөҪөгCәНөгEөДЧшұкЈ»
ЈЁ2Ј©ИзНј1ЛщКҫЈә№эөгAЧчAFЎНBDУЪөгFЈ®УЙРэЧӘөДРФЦКҝЙЦӘЈәAB=ADЈ¬ЎПBAD=60ЎгЈ¬ТАҫЭөИСьИэҪЗРОИэПЯәПТ»өДРФЦКҝЙЦӘЎПBAF=30ЎгЈ¬ЙиBF=aЈ¬ФтAF=$\sqrt{3}$aЈ¬УЪКЗҝЙөГөҪөгBөДЧшұкЈЁУГә¬aөДКҪЧУұнКҫЈ©Ј¬Ҫ«өгBөДЧшұкҙъИлЕЧОпПЯөДҪвОцКҪҝЙЗуөГaөДЦөЈ¬УЙaөДЦөҝЙөГөҪBDЎўAFөДіӨЈ¬ҙУ¶шҝЙЗуөГЎчABDөДГж»эЈ»
ЈЁ3Ј©өұөгDФЪyЦбЙПКұЈ¬УЙРэЧӘөДРФЦКҝЙЦӘЎПBAD=ЎПBЎдADЎд=60ЎгЈ¬УЪКЗҝЙЗуөГЦұПЯABөДҪвОцКҪЈ¬И»әуЗуөГЦұПЯABУлЕЧОпПЯөДҪ»өгЧшұкјҙҝЙөГіцөгBөДЧшұкЈ»өұөгDФЪxЦбЙПКұЈ¬№эөгBЧчBGЎНxЦбУЪөгGЈ¬УЙРэЧӘөДРФЦКҝЙЦӘЈәЎПABC=ЎПADEЈ¬ҪУПВАҙҝЙЦӨГчЎчABFЎЧЎчCDFЈ¬УЙПаЛЖИэҪЗРОөДРФЦКҝЙЦӘЎПFCD=ЎПBAF=60ЎгЈ¬ЙиCG=xЈ¬ФтBG=$\sqrt{3}$xЈ¬УЪКЗҝЙЗуөГөгBөДЧшұкЈЁУГә¬xөДКҪЧУұнКҫЈ©Ј¬Ҫ«өгBөДЧшұкҙъИлЕЧОпПЯөДҪвОцКҪҝЙЗуөГxөДЦөЈ¬ҙУ¶шЗуөГөгBөДЧшұкЈ®
Ҫвҙр ҪвЈәЈЁ1Ј©УЙРэЧӘөДРФЦКҝЙЦӘЈ»AC=AEЈ¬ЎПCAE=60ЎгЈ®
УЦЎЯAC=AEЈ¬AOЎНCEЈ¬
ЎаOC=OEЈ¬ЎПCAO=ЎПEAO=30ЎгЈ®
Ўа$\frac{OC}{OA}$=$\frac{\sqrt{3}}{3}$Ј¬јҙ$\frac{OC}{3}=\frac{\sqrt{3}}{3}$Ј®
ЎаOC=$\sqrt{3}$Ј®
ЎаCЈЁ-$\sqrt{3}$Ј¬0Ј©ЎўEЈЁ$\sqrt{3}$Ј¬0Ј©Ј®
ЈЁ2Ј©ИзНј1ЛщКҫЈә№эөгAЧчAFЎНBDУЪөгFЈ®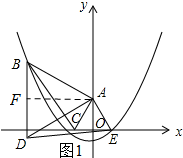
ЎЯAB=ADЈ¬AFЎНBDЈ¬ЎПBAD=60ЎгЈ¬
ЎаЎПBAF=30ЎгЈ®
ЙиBF=aЈ¬ФтAF=$\sqrt{3}$aЈ¬
ЎЯBDЎНxЦбЈ¬
ЎаBЈЁ-$\sqrt{3}$aЈ¬a+3Ј©Ј®
°СBЈЁ-$\sqrt{3}$aЈ¬a+3Ј©ҙъИлy=$\frac{2}{9}$x2+$\frac{\sqrt{3}}{9}$x-1өГЈә$\frac{2}{9}$ЈЁ-$\sqrt{3}$aЈ©2+$\frac{\sqrt{3}}{9}$ЈЁ-$\sqrt{3}$aЈ©-1=a+3Ј¬
ҪвөГЈәx1=$\sqrt{7}$+1Ј¬x2=-$\sqrt{7}$+1ЈЁЙбИҘЈ©Ј®
ЎаBD=2a=2$\sqrt{7}$+2Ј¬AF=$\sqrt{21}$+$\sqrt{3}$Ј®
ЎаSЎчABD=$\frac{1}{2}$BDЎБAF=$\frac{1}{2}$ЎБЈЁ2$\sqrt{7}$+2Ј©ЈЁ$\sqrt{21}$+$\sqrt{3}$Ј©=8$\sqrt{3}$+2$\sqrt{21}$Ј®
ЈЁ3Ј©өұөгDФЪyЦбЙПКұЈ¬ИзНј2ЛщКҫЈә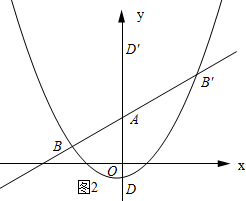
ЎЯУЙРэЧӘөДРФЦКҝЙЦӘЎПBAD=ЎПBЎдADЎд=60ЎгЈ®
ЎаЦұПЯABУлyЦбөДјРҪЗОӘ60ЎгЈ¬
ЙиЦұПЯABөДҪвОцКҪОӘЈәy=$\frac{\sqrt{3}}{3}$x+bЈ¬Ҫ«өгAөДЧшұкҙъИлөГЈәb=3Ј¬
ЎаЦұПЯABөДҪвОцКҪОӘy=$\frac{\sqrt{3}}{3}$x+3Ј®
Ҫ«y=$\frac{\sqrt{3}}{3}$x+3Улy=$\frac{2}{9}$x2+$\frac{\sqrt{3}}{9}$x-1БӘБўөГЈә$\frac{\sqrt{3}}{3}$x+3=$\frac{2}{9}$x2+$\frac{\sqrt{3}}{9}$x-1Ј®
ҪвөГЈәx1=-2$\sqrt{3}$Ј¬x2=3$\sqrt{3}$Ј¬
Ҫ«x=-2$\sqrt{3}$ҙъИлy=$\frac{\sqrt{3}}{3}$x+3өГЈәy=1Ј¬Ҫ«x=3$\sqrt{3}$ҙъИлy=$\frac{\sqrt{3}}{3}$x+3өГЈәy=6Ј¬
ЎаB1ЈЁ-2$\sqrt{3}$Ј¬1Ј©Ј¬B2ЈЁ3$\sqrt{3}$Ј¬6Ј©Ј®
өұөгDФЪxЦбЙПКұЈ¬ИзНј3ЛщКҫЈә№эөгBЧчBGЎНxЦбУЪөгGЈ¬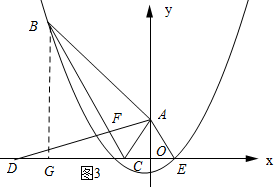
УЙРэЧӘөДРФЦКҝЙЦӘЈәЎПABC=ЎПADEЈ®
УЦЎЯЎПAFB=ЎПDFCЈ¬
ЎаЎчABFЎЧЎчCDFЈ®
ЎаЎПFCD=ЎПBAF=60ЎгЈ®
ЙиCG=xЈ¬ФтBG=$\sqrt{3}$xЈ®
ЎаөгBөДЧшұкОӘЈЁ-$\sqrt{3}$-xЈ¬$\sqrt{3}x$Ј©Ј®
Ҫ«өгBөДЧшұкҙъИлЕЧОпПЯөДҪвОцКҪөГЈә$\frac{2}{9}ЈЁ-\sqrt{3}-xЈ©^{2}$+$\frac{\sqrt{3}}{9}$ЈЁ-$\sqrt{3}$-xЈ©-1=$\sqrt{3}$xЈ®
Ўаx1=$\frac{3\sqrt{3}+\sqrt{39}}{2}$Ј¬x2=$\frac{3\sqrt{3}-\sqrt{39}}{2}$Ј®
ЎаB3ЈЁ$\frac{-5\sqrt{3}-\sqrt{39}}{2}$Ј¬$\frac{9+3\sqrt{13}}{2}$Ј©ЎўB4ЈЁ$\frac{-5\sqrt{3}+\sqrt{39}}{2}$Ј¬$\frac{9-3\sqrt{13}}{2}$Ј©Ј®
ЧЫЙПЛщКцЈ¬өұөгDФЪЧшұкЦбЙПКұЈ¬өгBөДЧшұкОӘB1ЈЁ-2$\sqrt{3}$Ј¬1Ј©ЎўB2ЈЁ3$\sqrt{3}$Ј¬6Ј©ЎўB3ЈЁ$\frac{-5\sqrt{3}-\sqrt{39}}{2}$Ј¬$\frac{9+3\sqrt{13}}{2}$Ј©ЎўB4ЈЁ$\frac{-5\sqrt{3}+\sqrt{39}}{2}$Ј¬$\frac{9-3\sqrt{13}}{2}$Ј©Ј®
өгЖА ұҫМвЦчТӘҝјІйөДКЗ¶юҙОәҜКэөДЧЫәПУҰУГЈ¬ҪвҙрұҫМвЦчТӘУҰУГБЛРэЧӘөДРФЦКЎўөИСьИэҪЗРОИэПЯәПТ»өДРФЦКЎўМШКвИсҪЗИэҪЗәҜКэЦөөДУҰУГЎўәҜКэНјПуЙПөгөДЧшұкУләҜКэҪвОцКҪөД№ШПөЈ¬УГә¬ЧЦДёөДКҪЧУұнКҫөгBөДЧшұкКЗҪвМвөД№ШјьЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
 ИзНјЈ¬КэЦбЙПұнКҫ1Ўў$\sqrt{3}$өД¶ФУҰөг·ЦұрОӘөгAЎўөгBЈ®ИфөгAКЗBCөДЦРөгЈ¬ФтөгCЛщұнКҫөДКэОӘЈЁЎЎЎЎЈ©
ИзНјЈ¬КэЦбЙПұнКҫ1Ўў$\sqrt{3}$өД¶ФУҰөг·ЦұрОӘөгAЎўөгBЈ®ИфөгAКЗBCөДЦРөгЈ¬ФтөгCЛщұнКҫөДКэОӘЈЁЎЎЎЎЈ©| AЈ® | $\sqrt{3}-1$ | BЈ® | 1-$\sqrt{3}$ | CЈ® | $\sqrt{3}-2$ | DЈ® | 2-$\sqrt{3}$ |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
 ИзНјЈ¬ЕЧОпПЯy=ax2+bx+cУлxЦбҪ»УЪAЎўBБҪөгЈ¬УлyЦбҪ»УЪөгCЈ¬Жд¶ФіЖЦбУлxЦбөДҪ»өгОӘDЈ¬ТСЦӘAЈЁ-1Ј¬0Ј©Ј¬CЈЁ0Ј¬2Ј©ЗТtanЎПABC=$\frac{1}{2}$Ј»
ИзНјЈ¬ЕЧОпПЯy=ax2+bx+cУлxЦбҪ»УЪAЎўBБҪөгЈ¬УлyЦбҪ»УЪөгCЈ¬Жд¶ФіЖЦбУлxЦбөДҪ»өгОӘDЈ¬ТСЦӘAЈЁ-1Ј¬0Ј©Ј¬CЈЁ0Ј¬2Ј©ЗТtanЎПABC=$\frac{1}{2}$Ј»Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
 ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬OОӘЧшұкФӯөгЈ¬өгAөДЧшұкОӘЈЁ5Ј¬0Ј©Ј¬БвРОOABCөД¶ҘөгBЈ¬C¶јФЪөЪТ»ПуПЮЈ¬tanЎПAOC=$\frac{4}{3}$Ј¬Ҫ«БвРОИЖөгA°ҙЛіКұХл·ҪПтРэЧӘҪЗҰБЈЁ0ЎгЈјЎПҰБЈјЎПAOCЈ©өГөҪБвРОFADEЈЁөгOөД¶ФУҰөгОӘөгFЈ©Ј¬EFУлOCҪ»УЪөгGЈ¬Б¬ҪбAGЈ®
ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬OОӘЧшұкФӯөгЈ¬өгAөДЧшұкОӘЈЁ5Ј¬0Ј©Ј¬БвРОOABCөД¶ҘөгBЈ¬C¶јФЪөЪТ»ПуПЮЈ¬tanЎПAOC=$\frac{4}{3}$Ј¬Ҫ«БвРОИЖөгA°ҙЛіКұХл·ҪПтРэЧӘҪЗҰБЈЁ0ЎгЈјЎПҰБЈјЎПAOCЈ©өГөҪБвРОFADEЈЁөгOөД¶ФУҰөгОӘөгFЈ©Ј¬EFУлOCҪ»УЪөгGЈ¬Б¬ҪбAGЈ®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
| AЈ® | -x2+2 | BЈ® | x3+4 | CЈ® | x3-4x+4 | DЈ® | x3-2x2-2x+4 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
| AЈ® | -1 | BЈ® | -2 | CЈ® | -3 | DЈ® | -4 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәМоҝХМв
 ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬БвРОOABCөДГж»эОӘ12Ј¬өгBФЪyЦбЙПЈ¬өгCФЪ·ҙұИАэәҜКэy=$\frac{k}{x}$өДНјПуЙПЈ¬ФтkөДЦөОӘ-6Ј®
ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬БвРОOABCөДГж»эОӘ12Ј¬өгBФЪyЦбЙПЈ¬өгCФЪ·ҙұИАэәҜКэy=$\frac{k}{x}$өДНјПуЙПЈ¬ФтkөДЦөОӘ-6Ј®Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com