
分析 (1)先根据非负数的性质列出方程,再得出m,n的值;
(2)根据线段的和差,可得AP,PB的长,根据线段中点的性质,可得PQ的长,根据线段的和差,可得答案.
解答 解:(1)由(m-6)2+2|n-m+4|=0,得
m-6=0,n-m+4=0.
解得m=6,n=2;
(2)由(1)得AB=6,AP=2PB,
有两种情况:
①当点P在点B的左侧时,如图1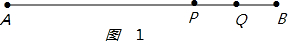 ,
,
AB=AP+PB=6,AP=2PB,
3PB=6,
解得PB=2,AP=2PB=2×2=4.
∵点Q为PB的中点,
∴PQ=$\frac{1}{2}$PB=1,
AQ=AP+PQ=4+1=5;
②当点P在点B的右侧时,如图2 ,
,
∵AP=AB+BP,AP=2PB,
∴2PB=6+PB,∴PB=6.
∵点Q为PB的中点,
∴BQ=$\frac{1}{2}$PB=3,
∴AQ=AB+BQ=6+3=9.
点评 本题考查了两点间的距离,利用非负数的和为零得出每个非负数同时为零是解题关键;利用线段的和差是解题关键,要分类讨论,以防遗漏.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
| A | B | C | D | E |
| -2 | +2.5 | -0.2 | +0.5 | -0.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com