
���� ��1����S=1+5+52+53+54+��+52011�����5S����5S-S�����4S��ֵ���������S��ֵ��
��2����S=1+$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+��+$\frac{1}{{3}^{10}}$����$\frac{1}{3}$S��ֵ��ͬ���ɵý����
��3����S=1+a+a2+a3+a4+��+an����aS��ֵ����aS-S�������a-1��S��ֵ���������S��ֵ��
��� �⣺��1����S=1+5+52+53+54+��+52011����5S=1+5+52+53+54+��+52011+52012��
��5S-S=��5+52+53+54+��+52011+52012��-��1+5+52+53+54+��+52011����
��4S=52012-1��
��S=$\frac{{5}^{2012}-1}{4}$��
��1+5+52+53+54+��+52011=$\frac{{5}^{2012}-1}{4}$��
��2����S=1+$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+��+$\frac{1}{{3}^{10}}$����$\frac{1}{3}$S=$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+��+$\frac{1}{{3}^{10}}$+$\frac{1}{{3}^{11}}$��
��S-$\frac{1}{3}$S=��1+$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+��+$\frac{1}{{3}^{10}}$��-��$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+��+$\frac{1}{{3}^{10}}$+$\frac{1}{{3}^{11}}$����
$\frac{2}{3}$S=1-$\frac{1}{{3}^{11}}$��
S=$\frac{3}{2}$-$\frac{1}{2��{3}^{10}}$��
��1+$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+��+$\frac{1}{{3}^{10}}$=$\frac{3}{2}-\frac{1}{2��{3}^{10}}$��
��3����S=1+a+a2+a3+a4+��+an����aS=a+a2+a3+a4+��+an+an+1��
��aS-S=��a+a2+a3+a4+��+an+an+1��-��1+a+a2+a3+a4+��+an��=an+1-1��
��S=$\frac{{a}^{n+1}-1}{a-1}$��
���� ������������Ĺ����⣬Ҳ��ͬ�����ݵij˷������������������ô�λ��������������ֵ���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���������ƫ���λ���ˣ� | -10 | -5 | 0 | +5 | +10 | +15 |
| ���� | 1 | 5 | 5 | 6 | 2 | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ��D�ǡ�ABC�ı�BC�ϵ�һ�㣬��AB=BD=AD=DC�����B����C����BAC����DAC�Ķ�����
��֪����ͼ��D�ǡ�ABC�ı�BC�ϵ�һ�㣬��AB=BD=AD=DC�����B����C����BAC����DAC�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
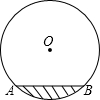 ��ͼ��ˮƽ���õ�Բ������ˮ�ܵ��Ľ���ֱ����1m������ˮ��Ŀ�ABΪ0.6m��
��ͼ��ˮƽ���õ�Բ������ˮ�ܵ��Ľ���ֱ����1m������ˮ��Ŀ�ABΪ0.6m���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
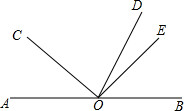 ��ͼ����O��ֱ��AB��һ�㣬ODƽ�֡�BOC����COE=90�㣮
��ͼ����O��ֱ��AB��һ�㣬ODƽ�֡�BOC����COE=90�㣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com