
【题目】如图所示,点D是等边△ABC内一点,DA=15,DB=19,DC=21,将△ABD绕点A逆时针旋转到△ACE的位置,当点E在BD的延长线上时.
求(1)∠BDA的度数;
(2)△DEC的周长.

【答案】(1)∠BDA=120°;(2)55.
【解析】
(1)先根据等边三角形的性质得∠BAC=60°,AB=AC,再根据旋转的性质得到AD=AE,CE=BD=19,∠DAE=∠BAC=60°,则可判断△ADE为等边三角形,得出∠ADE=60°,即可得出答案;
(2)由DE=AD=15,CE=DB=19,即可计算△DEC的周长.
解:(1)∵△ABC为等边三角形,
∴∠BAC=60°,AB=AC,
∵△ABD绕点A逆时针旋转到△ACE的位置,点E在BD的延长线上,
∴AD=AE,CE=DB=19,∠DAE=∠BAC=60°,
∴△ADE为等边三角形,
∴∠ADE=60°,DE=AD=15,
∴∠BDA=120°;
(2)△DEC的周长=DE+DC+CE=15+21+19=55.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】抛物线经过A![]() ,B
,B![]() ,C
,C![]() 三点.
三点.
(1)求抛物线的解析式。
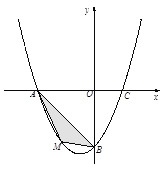
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年的北京世园会在北京延庆区成功举办,这是我国举办的级别最高、规模最大的国际性博览会,吸引了各地的游客前来参观.会展期间延庆某宾馆有50间房供游客居住,当每间房每天定价为380元时,宾馆会住满;当每间房每天定价每增加20元时,就会空闲一间房,如果有游客居住,宾馆需对居住的每间房每天支出30元的费用,当房价定为多少元时,宾馆当天的利润为20250元?设房价比定价380元增加x元,则有( )
A.(x+380)(50﹣![]() )﹣50×30=20250
)﹣50×30=20250
B.(380+x﹣30)(50﹣![]() )=20250
)=20250
C.x(50﹣![]() )﹣50×30=20250
)﹣50×30=20250
D.(x﹣30)(50﹣![]() )=20250
)=20250
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
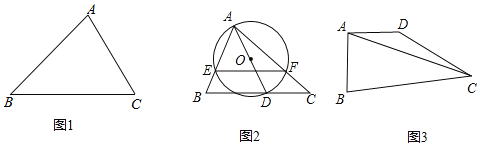
(1)如图1,在△ABC中,∠A=75°,∠C=60°,AC=6![]() ,求△ABC的外接圆半径R的值;
,求△ABC的外接圆半径R的值;
问题探究
(2)如图2,在△ABC中,∠BAC=60°,∠C=45°,AC=8![]() ,点D为边BC上的动点,连接AD以AD为直径作⊙O交边AB、AC分别于点E、F,接E、F,求EF的最小值;
,点D为边BC上的动点,连接AD以AD为直径作⊙O交边AB、AC分别于点E、F,接E、F,求EF的最小值;
问题解决
(3)如图3,在四边形ABCD中,∠BAD=90°,∠BCD=30°,AB=AD,BC+CD=12![]() ,连接AC,线段AC的长是否存在最小值,若存在,求最小值:若不存在,请说明理由.
,连接AC,线段AC的长是否存在最小值,若存在,求最小值:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上,直线
的图象上,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴相交于
轴相交于![]() 、
、![]() 两点.
两点.
(1)求直线![]() 的解析式:
的解析式:
(2)求![]() 、
、![]() 两点坐标;
两点坐标;
(3)连接![]() 、
、![]() ,记
,记![]() 的面积为
的面积为![]() 、
、![]() 面积为
面积为![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小菁同学在数学实践活动课中测量路灯的高度.如图,已知她的目高AB为1.5米,她先站在A处看路灯顶端O的仰角为35°,再往前走3米站在C处,看路灯顶端O的仰角为65°,则路灯顶端O到地面的距离约为( )
(已知sin35°≈0.6,cos35°≈0.8,tan35°≈0.7,sin65°≈0.9,cos65°≈0.4,tan65°≈2.1)

A.3.2米B.3.9米C.4.7米D.5.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,D是AC边上一点,连接BD,将△BCD绕点B逆时针旋转60°得到△BAE,连接ED,若BC=5,BD=4,有下列结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△ADE的周长是9.其中正确的个数是( )
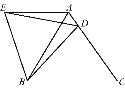
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,以A为圆心,AB为半径作 ![]() ,交对角线AC于点E,连结BE并延长交CD于点F,记图中分割部分的面积为S1,S2.则下列对S1与S2的大小关系判断正确的是( )
,交对角线AC于点E,连结BE并延长交CD于点F,记图中分割部分的面积为S1,S2.则下列对S1与S2的大小关系判断正确的是( )

A.S1>S2B.S1<S2C.S1=S2D.与正方形ABCD的边长有关
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com