
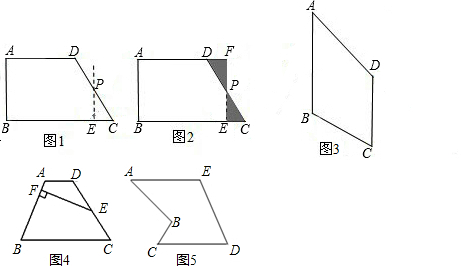
分析 思考与实践:
(1)根据矩形的定义:有一个角是直角的平行四边形是矩形进行判断即可;
(2)取AD的中点P,过点P做PE∥BC交AB于E,交CD的延长线于F,根据旋转后三角形的一条边与四边形的一边在同一条直线上,构成平行四边形.
发现与运用:
(1)过点E作AB的平行线,交BC于点G,交AD的延长线于点H,得出S梯形ABCD=S□ABGH即可;
(2)分别取AB、BC的中点F、H,作直线FH,分别交AE、CD于点M、N,将△AMF与△CNH一起拼接到△FBH位置即可.
解答 解:(Ⅰ)(1)如图2所示,△PEC绕点P逆时针旋转180°到△PFD的位置,易知PE与PF在同一条直线上,
∴EF∥AB,
又∵在梯形ABCD中,AD∥BC,∠C+∠ADP=180°,
∴∠FDP+∠ADP=180°,
∴AD和DF在同一条直线上,那么构成的新图形是一个四边形,
又∵AD∥BC,
∴四边形ABEF是一个平行四边形,
∵∠A=90°,
∴拼成的新图形是矩形.
故答案为:矩形;
(2)如图所示,取AD的中点P,过点P做PE∥BC交AB于E,交CD的延长线于F,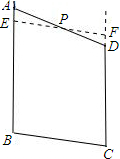
△PEA绕点P逆时针旋转180°到△PFD的位置,易知PE与PF在同一条直线上,
所以EF∥BC,
由于图中AB∥CD
所以图中四边形BCFE是平行四边形.
(Ⅱ)(1)如下图所示,过点E作AB的平行线,交BC于点G,交AD的延长线于点H,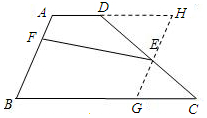
∵AH∥CG,
∴∠H=∠CGE,
∵E是CD的中点,
∴DE=CE,
又∵∠DEH=∠CEG,
∴△DEH≌△CEG(AAS),
∴S△DEH=S△CEG,
∵AH∥BC,AB∥HC,
∴四边形ABGH是平行四边形,
∵EF⊥AB于点F,AB=5,EF=4,
∴平行四边形ABGH的面积=AB×EF=5×4=20,
∴梯形ABCD的面积=五边形ABGEDD的面积+△CEG的面积=五边形ABGEDD的面积+△DEH的面积=平行四边形ABGH的面积=20;
(2)能.
如图5,分别取AB、BC的中点F、H,作直线FH,分别交AE、CD于点M、N,将△AMF与△CNH一起拼接到△FBH位置即可.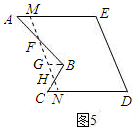
点评 本题考查了旋转的性质、平行四边形及矩形的判定与性质以及割补法的运用.解决问题的关键是作辅助线构造全等三角形以及平行四边形,根据平行四边形的性质以及全等三角形的性质得出结论.解题时注意:两角及其中一个角的对边对应相等的两个三角形全等.


科目:初中数学 来源: 题型:解答题
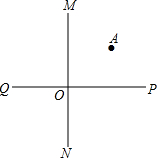 如图所示,直线MN⊥PQ,垂足是点O,点A是∠POM内部的任意一点.
如图所示,直线MN⊥PQ,垂足是点O,点A是∠POM内部的任意一点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
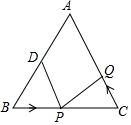 △ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为( )
△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为( )| A. | 2 | B. | 5 | C. | 1或5 | D. | 2或3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 关于直线对称的两个三角形一定全等 | |
| B. | 两个圆形纸片随意平放在水平桌面上构成轴对称图形 | |
| C. | 若两图形关于直线对称,则对称轴是对应点所连线的垂直平分线 | |
| D. | 等腰三角形一边上的高,中线及这边对角平分线重合 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>0 | B. | x≠3 | C. | x>0且x≠3 | D. | x≥0且x≠3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≥-3 | B. | m>-3且m≠6 | C. | m≥-3且m≠6 | D. | m≠6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com