
| A. | m<4 | B. | m>4 | C. | m<4且m≠2 | D. | m>0且m≠2 |
科目:初中数学 来源: 题型:填空题
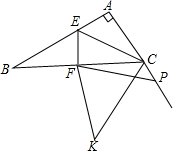 在△ABC中,∠BAC=90°,BC的垂直平分线EF交BC于点F,交AB于点E,P是AC延长线上一点,连接FP,将FP绕点F逆时针旋转2α,得到FK,连接CK,如果∠B=α(0°<α<90°),则$\frac{CK-CP}{cosα•EF}$=2.
在△ABC中,∠BAC=90°,BC的垂直平分线EF交BC于点F,交AB于点E,P是AC延长线上一点,连接FP,将FP绕点F逆时针旋转2α,得到FK,连接CK,如果∠B=α(0°<α<90°),则$\frac{CK-CP}{cosα•EF}$=2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两位同学住在同一小区,在同一中学读书,一天恰好在同一时间骑自行车沿同一线路上学,小区离学校有9km,甲以匀速行驶,花了30min到校,乙的行程信息如图中折线O-A-B-C所示,分别用y1,y2表示甲、乙在时间x(min)时的行程,请回答下列问题:
甲、乙两位同学住在同一小区,在同一中学读书,一天恰好在同一时间骑自行车沿同一线路上学,小区离学校有9km,甲以匀速行驶,花了30min到校,乙的行程信息如图中折线O-A-B-C所示,分别用y1,y2表示甲、乙在时间x(min)时的行程,请回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 捐款(元) | 20 | 40 | 50 | 100 |
| 人数 | 10 | 8 |
| A. | $\left\{\begin{array}{l}{x+y=22}\\{40x+50y=2000}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=22}\\{50x+40y=2000}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=22}\\{40x+50y=1000}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=22}\\{50x+40y=1000}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com