
【题目】如图,长方形ABCD中,M为CD中点,分别以点B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P.若∠PMC=110°,则∠BPC的度数为( ) 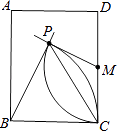
A.35°
B.45°
C.55°
D.65°
【答案】C
【解析】解:∵以B、M为圆心,分别以BC长、MC长为半径的两弧相交于P点, ∴BP=BC,MP=MC,
∵∠PMC=110°,
∴∠MCP= ![]() (180°﹣∠PMC)=
(180°﹣∠PMC)= ![]() (180°﹣110°)=35°,
(180°﹣110°)=35°,
在长方形ABCD中,∠BCD=90°,
∴∠BCP=90°﹣∠MCP=90°﹣35°=55°,
∴∠BCP=∠BPC=55°.
故选C.
【考点精析】认真审题,首先需要了解线段垂直平分线的性质(垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等),还要掌握矩形的性质(矩形的四个角都是直角,矩形的对角线相等)的相关知识才是答题的关键.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】为了了解市民“获取新闻的最主要途径”某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图. 
根据以上信息解答下列问题:
(1)这次接受调查的市民总人数是;
(2)扇形统计图中,“电视”所对应的圆心角的度数是;
(3)请补全条形统计图;
(4)若该市约有80万人,请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y= ![]() (k≠0)的图象交于第二、第四象限内的A,B两点,与y轴交于C点,过A作AH⊥y轴,垂足为H,AH=4,tan∠AOH=
(k≠0)的图象交于第二、第四象限内的A,B两点,与y轴交于C点,过A作AH⊥y轴,垂足为H,AH=4,tan∠AOH= ![]() ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2). 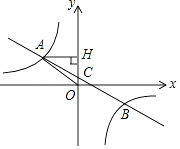
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=45°,AB=AC,D为△ABC内一点,AD=4,如果把△ABD绕点A按逆时针方向旋转,使AB与AC重合,求点D运动的路径长. 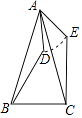
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的顶点坐标为A(﹣2,3)、B(﹣3,1)、C(﹣1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C′,点B′、C′分别是点B、C的对应点. 
(1)求过点B′的反比例函数解析式;
(2)求线段CC′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() 的图象相交于点A(﹣2,1),点B(1,n).
的图象相交于点A(﹣2,1),点B(1,n). 
(1)求此一次函数和反比例函数的解析式;
(2)请直接写出满足不等式kx+b﹣ ![]() <0的解集;
<0的解集;
(3)在平面直角坐标系的第二象限内边长为1的正方形EFDG的边均平行于坐标轴,若点E(﹣a,a),如图,当曲线y= ![]() (x<0)与此正方形的边有交点时,求a的取值范围.
(x<0)与此正方形的边有交点时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)请画出△A1B1C1 , 使△A1B1C1与△ABC关于x轴对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2 , 并直接写出点B旋转到点B2所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为( )
A.x1=0,x2=4
B.x1=1,x2=5
C.x1=1,x2=﹣5
D.x1=﹣1,x2=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,动点M从点A出发,以每秒1个单位长度的速度沿AB向点B匀速运动;同时,动点N从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动,过线段MN的中点G作边AB的垂线,垂足为点G,交△ABC的另一边于点P,连接PM,PN,当点N运动到点A时,M,N两点同时停止运动,设运动时间为t秒.
(1)当t=秒时,动点M,N相遇
(2)设△PMN的面积为S,求S与t之间的函数关系式
(3)取线段PM的中点K,连接KA,KC,在整个运动过程中,△KAC的面积是否变化?若变化,直接写出它的最大值和最小值;若不变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com