
【题目】如图,已知AD⊥BC,EG⊥BC,垂足分别为D、G、AD平分∠BAC,求证:∠E=∠4.
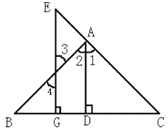
证明:∵AD⊥BC,EG⊥BC(已知)
∴AD∥EG( )
∴∠2=∠3( )
∠1= (两直线平行,同位角相等)
∵AD平分∠BAC(已知)
∴∠1=∠2( )
∴∠E=∠3( )
∵∠3=∠4( )
∴∠E=∠4(等量代换)
科目:初中数学 来源: 题型:
【题目】为了解某校七年级学生参加“数学素养水平测试”的成绩情况,在全段学生中抽查一部分学生的成绩,整理后按A、B、C、D四个等级绘制成如下两幅统计图(部分项目不完整).
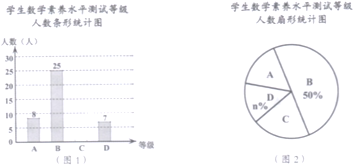
(1)根据统计图所提供的信息,得出抽查学生共有 人,图2中![]() .
.
(2)补全条形统计图1,图2中等级C所对应的扇形的圆心角度数为 .
(3)该校共有800名七年级学生参加素养水平测试,请估算等级A的学生人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015桂林)“全民阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1520元,20本文学名著比20本动漫书多440元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)求每本文学名著和动漫书各多少元?
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于72本,总费用不超过2000元,请求出所有符合条件的购书方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”,设BC=a,AC﹣b,AB=c.
【特例探索】
(1)如图1,当∠ABE=45°,c=2![]() 时,a= ,b= ;如图2,当∠ABE=30°,c=4时,a= ,b= ;
时,a= ,b= ;如图2,当∠ABE=30°,c=4时,a= ,b= ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
【拓展应用】
(3)如图4,在ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2![]() ,AB=3.求AF的长.
,AB=3.求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AB边落在AC上,点B落在点H处,折痕AE分别交BC于点E,交BO于点F,连结FH,则下列结论(1)AD=DF;(2)![]() =
=![]() ;(3)
;(3)![]() =
=![]() ﹣1;(4)四边形BEHF为菱形.正确的有几个( )
﹣1;(4)四边形BEHF为菱形.正确的有几个( )
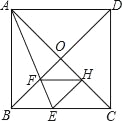
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 两地相距
两地相距![]() ,甲、乙二人分别骑自行车和摩托车沿相同路线匀速行驶,由
,甲、乙二人分别骑自行车和摩托车沿相同路线匀速行驶,由![]() 地到达
地到达![]() 地.他们行驶的路程
地.他们行驶的路程![]() 与甲出发后的时间
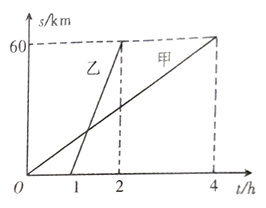
与甲出发后的时间![]() 之间的函数图像如图所示.
之间的函数图像如图所示.
(1)乙比甲晚出发几小时?乙比甲早到几小时?
(2)分别写出甲、乙行驶的路程![]() 与甲出发后的时间
与甲出发后的时间![]() 的函数关系式(不写自变量的取值范围).
的函数关系式(不写自变量的取值范围).
(3)乙在甲出发后几小时追上甲?追上甲的地点离![]() 地有多远?
地有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是把图1放入长方形内得到的,![]() ,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为___.
,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红同学要测量![]() ,
,![]() 两地的距离,但
两地的距离,但![]() ,
,![]() 之间有一水池,不能直接测量,于是她在
之间有一水池,不能直接测量,于是她在![]() ,
,![]() 同一水平面上选取了一点
同一水平面上选取了一点![]() ,点
,点![]() 可直接到达
可直接到达![]() ,
,![]() 两地.她测量得到
两地.她测量得到![]() 米,
米,![]() 米,
米,![]() .请你帮助小红同学求出
.请你帮助小红同学求出![]() ,
,![]() 两点之间的距离.
两点之间的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com