
【题目】如图中,AE⊥AB且AE=AB,BC⊥CD且BC=CD,若点E、B、D到直线AC的距离分别为6、3、2,则图中实线所围成的阴影部分面积S是( )

A.50B.44C.38D.32
【答案】D
【解析】
由已知和图形根据“K”字形全等,用AAS可证△FEA≌△MAB,△DHC≌△CMB,推出AM=EF=6,AF=BM=3, CM=DH=2,BM=CH=3,从而得出FH=14,根据阴影部分的面积=S梯形EFHD-S△EFA-S△ABC-S△DHC和面积公式代入求出即可.
∵AE⊥AB,EF⊥AF,BM⊥AM,

∴∠F=∠AMB=∠EAB=90°,
∴∠FEA+∠EAF=90°,∠EAF+∠BAM=90°,
∴∠FEA=∠BAM,
在△FEA和△MAB中
 ,
,
∴△FEA≌△MAB(AAS),
∴AM=EF=6,AF=BM=3,
同理CM=DH=2,BM=CH=3,
∴FH=3+6+2+3=14,
∴梯形EFHD的面积=![]() =
=![]() =56,
=56,
∴阴影部分的面积=S梯形EFHD-S△EFA-S△ABC-S△DHC
=![]()
=32.
故选:D.


科目:初中数学 来源: 题型:
【题目】用“◇”和“☆”分别代表甲种植物和乙种植物,为了美化环境,采用如图所示的方案种植.
(1)观察图形,寻找规律,并填写下表:


(2)求出第![]() 个图形中甲种植物和乙种植物的株数;
个图形中甲种植物和乙种植物的株数;
(3)是否存在一种种植方案,使得乙种植物的株数是甲种植物的株数的2倍?若存在,请你写出是第几个方案,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90,BC=4,AC=3,线段PQ⊥BC于Q(如图,此时点Q与点B重合),PQ=AB,当点P沿PB向B滑动时,点Q相应的从B沿BC向C滑动,始终保持PQ=AB不变,当△ABC与△PBQ全等时,PB的长度等于________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线).继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到![]() 条折痕,那么对折四次可以得到( )条折痕.如果对折
条折痕,那么对折四次可以得到( )条折痕.如果对折![]() 次, 可以得到( )条折痕
次, 可以得到( )条折痕
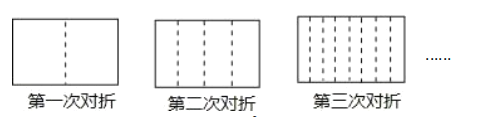
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=90°, AB//CD,M为BC边上的一点,AM平分∠BAD,DM平分∠ADC,

求证:(1) AM⊥DM;
(2) M为BC的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
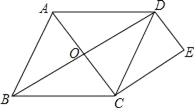
【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形;
(2)若AB=10,AC=12,求四边形CODE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC>AB.
(1)作AB边的垂直平分线交BC于点P,作AC边的垂直平分线交BC于点Q,连接AP,AQ.(尺规作图,保留作图痕迹,不需要写作法)
(2)在(1)的条件下,若BC=14,求△APQ的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芭蕾舞剧《吉赛尔》在城市剧院演出前,主办方工作人员准备利用![]() 米长的墙为一边,用
米长的墙为一边,用![]() 米隔栏绳作为另三边,设立一个面积为
米隔栏绳作为另三边,设立一个面积为![]() 平方米的长方形等候区,如图,为了方便观众进出,在与墙垂直的两边上留出一个进口和两个出口,宽度都为
平方米的长方形等候区,如图,为了方便观众进出,在与墙垂直的两边上留出一个进口和两个出口,宽度都为![]() 米,问围成的这个长方形的相邻两边长分别是多少?
米,问围成的这个长方形的相邻两边长分别是多少?

解:令这个长方形垂直于墙的一边为宽,平行于墙的一边为长;设这个长方形的宽为![]() 米,则长为_____________米.(完成填空后继续解题)
米,则长为_____________米.(完成填空后继续解题)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
利用完全平方公式,可以将多项式ax2+bx+c(a≠0)变形为a(x+m)2+n的形式,我们把这样的变形方法叫做多项式ax2+bx+c的配方法.
运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
例如:x2+11x+24=![]()
=![]()
=![]()
=(x+8)(x+3)
根据以上材料,解析下列问题:
(1)用多项式的配方法将x2+8x﹣1化成(x+m)2+n的形式;
(2)求证:x,y取任何实数时,多项式x2+y2﹣2x﹣4y+16的值总为正数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com