
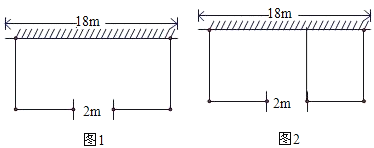
【题目】如图1,若要建一个长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米.
求:(1)若鸡场面积150平方米,鸡场的长和宽各为多少米?
(2)鸡场面积可能达到200平方米吗?
(3)如图2,若在鸡场内要用竹篱笆加建一道隔栏,则鸡场最大面积可达多少平方米?
【答案】(1)长为15米,宽为10米;(2)不可能达到200平方米;(3)![]()
【解析】
(1)若鸡场面积150平方米,求鸡场的长和宽,关键是用一个未知数表示出长或宽,并注意去掉门的宽度;
(2)求二次函数的最值问题,列出面积的关系式化为顶点式,确定函数最大值与200的大小关系,即可得到答案;
(3)此题中首先设出鸡场的面积和宽,列函数式时要注意墙宽有三条道,所以鸡场的长要用篱笆的周长减去3个宽再加上大门的宽2米,再求函数式的最大值.
(1)设宽为x米,则:x(33﹣2x+2)=150,
解得:x1=10,x2=![]() (不合题意舍去),
(不合题意舍去),
∴长为15米,宽为10米;
(2)设面积为w平方米,则:W=x(33﹣2x+2),
变形为: ![]() ,
,
∴鸡场面积最大值为![]() =153
=153![]() <200,即不可能达到200平方米;
<200,即不可能达到200平方米;
(3)设此时面积为Q平方米,宽为x米,则:Q=x(33﹣3x+2),
变形得:Q=﹣3(x-![]() )2+
)2+ ![]() ,
,
∴此时鸡场面积最大值为![]() .
.


科目:初中数学 来源: 题型:
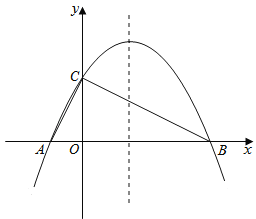
【题目】如图,已知抛物线y=﹣![]() x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
(1)求抛物线的解析式及它的对称轴;
(2)求点C的坐标,连接AC、BC并求线段BC所在直线的解析式;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市有![]() ,
,![]() 两种型号的瓶子,其容量和价格如表,小张买瓶子用来分装15升油(瓶子都装满,且无剩油);当日促销活动:购买
两种型号的瓶子,其容量和价格如表,小张买瓶子用来分装15升油(瓶子都装满,且无剩油);当日促销活动:购买![]() 型瓶3个或以上,一次性返还现金5元,设购买
型瓶3个或以上,一次性返还现金5元,设购买![]() 型瓶
型瓶![]() (个),所需总费用为
(个),所需总费用为![]() (元),则下列说法不一定成立的是( )
(元),则下列说法不一定成立的是( )
型号 | A | B |
单个盒子容量(升) | 2 | 3 |
单价(元) | 5 | 6 |
A.购买![]() 型瓶的个数是
型瓶的个数是![]() 为正整数时的值B.购买
为正整数时的值B.购买![]() 型瓶最多为6个
型瓶最多为6个
C.![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() D.小张买瓶子的最少费用是28元
D.小张买瓶子的最少费用是28元
查看答案和解析>>
科目:初中数学 来源: 题型:
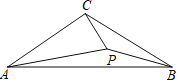
【题目】如图,若![]() 内一点
内一点![]() 满足
满足![]() ,则称点
,则称点![]() 为
为![]() 的布罗卡尔点,三角形的布罗卡尔点是法国数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知
的布罗卡尔点,三角形的布罗卡尔点是法国数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的布罗卡尔点,若
的布罗卡尔点,若![]() ,则
,则![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 和直线
和直线![]() .我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.
.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.
下列判断: ①当x>2时,M=y2;
②当x<0时,x值越大,M值越大;
③使得M大于4的x值不存在;
④若M=2,则x= 1 .
其中正确的有

A.1个 B.2个 C. 3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
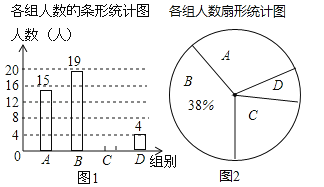
【题目】小明随机调查了若干市民租用共享单车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如下统计图(A:0<t≤10,B:10<t≤20,C:20<t≤30,D:t>30),根据图中信息,解答下列问题:
(1)这项被调查的总人数是多少人?
(2)试求表示A组的扇形统计图的圆心角的度数,补全条形统计图;
(3)如果小明想从D组的甲、乙、丙、丁四人中随机选择两人了解平时租用共享单车情况,请用列表或画树状图的方法求出恰好选中甲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
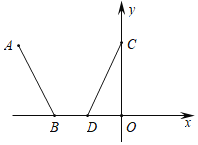
【题目】如图,已知A(﹣6,4),B(﹣4,0),将线段AB沿直线x=﹣3进行轴对称变换得到对应线段CD.
(1)直接写出C点的坐标为 ,D点的坐标为 ;
(2)将线段CD绕O点旋转180°得对应线段EF,请你画出线段EF;
(3)将线段EF沿y轴正方向平移m个单位,当m= 时,线段EF与CD成轴对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,B,C,D三点在![]() 上,
上,![]() ,PA是钝角△ABC的高线,PA的延长线与线段CD交于点E.
,PA是钝角△ABC的高线,PA的延长线与线段CD交于点E.
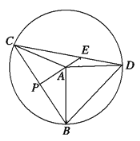
(1)请在图中找出一个与∠CAP相等的角,这个角是 ;
(2)用等式表示线段AC,EC,ED之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com