
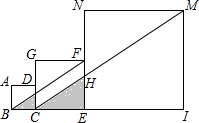
 正方形ABCD的边长为1,正方形CEFG边长为2,正方形EIMN边长为4,以后的正方形边长按此规律扩大,其中点B、C、E、I…在同一条直线上,连接BF交CG于点K,连接CM交EN于点H,记△BCK的面积为S1,△CEH的面积为S2,…,依此规律,Sn=$\frac{{2}^{2n-2}}{3}$.
正方形ABCD的边长为1,正方形CEFG边长为2,正方形EIMN边长为4,以后的正方形边长按此规律扩大,其中点B、C、E、I…在同一条直线上,连接BF交CG于点K,连接CM交EN于点H,记△BCK的面积为S1,△CEH的面积为S2,…,依此规律,Sn=$\frac{{2}^{2n-2}}{3}$. 分析 首先证明△BCK∽△CEH,得$\frac{{S}_{1}}{{S}_{2}}$=($\frac{1}{2}$)2,求出S1、S2、S3、…探究规律后即可解决问题.
解答 解:如图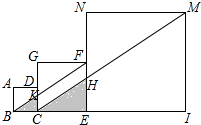 ,∵CK∥EF,
,∵CK∥EF,
∴$\frac{CK}{EF}$=$\frac{BC}{BE}$,
∴$\frac{CK}{2}$=$\frac{1}{3}$,
∴CK=$\frac{2}{3}$,
同理可得:EH=$\frac{4}{3}$,
∴$\frac{BC}{CE}$=$\frac{CK}{HE}$,
∵∠BCK=∠CEH=90°,
∴△BCK∽△CEH,
∴$\frac{{S}_{1}}{{S}_{2}}$=($\frac{1}{2}$)2,
∵S1=$\frac{1}{2}$•1•$\frac{2}{3}$=$\frac{1}{3}$,
∴S2=$\frac{1}{3}$•4,
S3=$\frac{1}{3}$•(4)2,
…
Sn=$\frac{1}{3}$•(4)n-1=$\frac{{2}^{2n-2}}{3}$.
故答案为$\frac{{2}^{2n-2}}{3}$.
点评 本题考查正方形的性质,相似三角形的判定和性质等知识,解题的关键是利用相似三角形的性质,记住相似三角形的面积比定义相似比的平方,属于中考常考题型.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:解答题
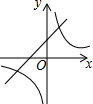 如图,一次函数y1=2x+2的图象与反比例函数y2=$\frac{k}{x}$(k为常数,且k≠0)图象都经过点A(m,3).
如图,一次函数y1=2x+2的图象与反比例函数y2=$\frac{k}{x}$(k为常数,且k≠0)图象都经过点A(m,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 25,25 | B. | 25,22 | C. | 20,22 | D. | 22,24 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
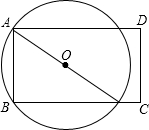 已知,如图,在矩形ABCD中,AB=6,BC=8,P点是线段BC上的任一动点,过点A、B、P作⊙O,设⊙O的半径为r,当⊙O与线段CD有且只有两个交点时,半径r的取值范围是$\frac{73}{16}$<r≤5.
已知,如图,在矩形ABCD中,AB=6,BC=8,P点是线段BC上的任一动点,过点A、B、P作⊙O,设⊙O的半径为r,当⊙O与线段CD有且只有两个交点时,半径r的取值范围是$\frac{73}{16}$<r≤5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
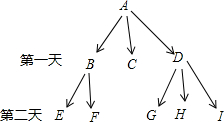 A同学心里有一个秘密,这个秘密按图中箭头指向在A,B,C,D,E,F,G,H,I这9个同学中传播,将这个秘密告诉过B的同学或者B将这个秘密告诉过的同学都不会再告诉B这个秘密.(注:不同的字母代表不同的同学)
A同学心里有一个秘密,这个秘密按图中箭头指向在A,B,C,D,E,F,G,H,I这9个同学中传播,将这个秘密告诉过B的同学或者B将这个秘密告诉过的同学都不会再告诉B这个秘密.(注:不同的字母代表不同的同学)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com