
����Ŀ���ס�������������ͬһ·�ߴ�A��ǰ��B�أ��׳���aǧ��/ʱ���ٶ�������ʻ��;�г��ֹ��Ϻ�ͣ��ά�ޣ��ú���2aǧ��/ʱ���ٶȼ�����ʻ���ҳ��ڼ׳�����2Сʱ������ǰ��B�أ��ȼ׳���30���ӵ������B�غ��ҳ���ԭ�ٶȷ���A�أ��׳���2aǧ��/ʱ���ٶȷ���A�أ���ס���������A�����s��ǧ�ף����׳��뿪A�ص�ʱ��Ϊt��Сʱ����s��t֮��ĺ���ͼ����ͼ��ʾ������˵������a=40���ڼ׳�ά������ʱ��Ϊ1Сʱ����������;�еڶ�������ʱt��ֵΪ5.25���ܵ�t=3ʱ���������40ǧ�ף����в���ȷ�ĸ���Ϊ��������

A. 0�� B. 1�� C. 2�� D. 3��
���𰸡�A
��������
�⣺���ɺ���ͼ��a=120��3=40��
�ʢ���ȷ��
�������⣬��5.5��3��120�£�40��2����
=2.5��1.5��
=1��
��׳�ά��ʱ��Ϊ1Сʱ��
�ʢ���ȷ��
����ͼ��

�׳�ά��ʱ����1Сʱ��
��B��4��120����
�����ڼ׳���2Сʱ������ǰ��B�أ��ȼ���30���ӵ��
��E��5��240����
������ʻ���ٶ�Ϊ��240��3=80��
���ҷ��ص�ʱ��Ϊ��240��80=3��
��F��8��0����
��BC�Ľ���ʽΪy1=k1t+b1��EF�Ľ���ʽΪy2=k2t+b2����ͼ��ã�
![]() ��
��![]() ��
��
���![]() ��
��![]() ��
��
��y1=80t��200��y2=��80t+640��
��y1=y2ʱ��
80t��200=��80t+640��
t=5.25��
��������;�еڶ�������ʱt��ֵΪ5.25Сʱ��
��Ū����ȷ��
�ܵ�t=3ʱ���׳��е�·��Ϊ��120km���ҳ��е�·��Ϊ��80����3��2��=80km��
����������·��Ϊ��120��80=40ǧ�ף�
�ʢ���ȷ��
��ѡ��A��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����![]() ��ͼ����y�ύ�ڵ�A��һ�κ���
��ͼ����y�ύ�ڵ�A��һ�κ���![]() ��ͼ����
��ͼ����![]() ����x�ύ�ڵ�C����
����x�ύ�ڵ�C����![]() ��ͼ���ڵ�D���ҵ�D������Ϊ
��ͼ���ڵ�D���ҵ�D������Ϊ![]() .
.
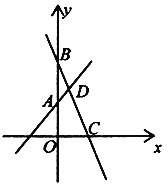
��1����k��b��ֵ��
��2����![]() ����x��ȡֵ��Χ��__________.
����x��ȡֵ��Χ��__________.
��3�����ı���![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
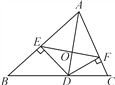
����Ŀ����ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��DF�ֱ��ǡ�ABD�͡�ACD�ĸߣ��õ������ĸ����ۣ���OA��OD����AD��EF���۵���BAC��90��ʱ���ı���AEDF�������Σ���AE2��DF2��AF2��DE2.������ȷ����_________��(�����)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��E��F��G��H�ֱ���OA��OB��OC��OD���е㣬��ô��ABCD���ı���EFGH�Ƿ���λ��ͼ�Σ�Ϊʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB=AC��BC=BD����![]() ����
����![]() ______.���ú�
______.���ú�![]() �Ĵ���ʽ��.
�Ĵ���ʽ��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ�����������һ��2��2������������ÿ�����ĺᡢ�������Ϊ��������֪��A(1��2)����ֱ��OA������ƽ��k����λ��Ҫʹ�ֲ���ƽ�ƺ��ֱ������ĸ������ͬ����k��ֵΪ�� ��
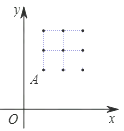
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��![]()
��2��![]()
��3��8x2��4(2x2��3x��1)
��4�� 5x2��2(3y2��5x2)��(��4y2��7xy)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���ÿ������Ϊ80Ԫ��ij����Ʒԭ����ÿ��100Ԫ���ۣ�һ����۳�100�������������г����飬����������Ʒ����ÿ����1Ԫ��������������10����
��1�����̳���Ӫ����Ʒԭ��һ��ɻ��������Ԫ��
��2�����������Ʒÿ������xԪ�����̳�һ��ɻ�����yԪ��
�����̳���Ӫ����Ʒһ��Ҫ������2160Ԫ����ÿ����ƷӦ���۶���Ԫ��
�����y��x֮��ĺ�����ϵʽ���������д����xȡ��ֵʱ���̳�����������2160Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵȱ������Σ�DΪBC����һ�����㣨D��B��C�����غϣ���AD=AE����DAE=60��������CE��
��1����֤����ABD�ա�ACE��
��2����AB=2�����ı���ADCE���ܳ�ȡ��Сֵʱ����BD�ij���

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com