
����Ŀ����ͼ�٣���ƽ��ֱ������ϵ�У����κ���y��![]() x2+bx+c��ͼ���������ύ��A��B��C���㣬���е�A������Ϊ����3��0������B������Ϊ��4��0��������AC��BC������P�ӵ�A���������߶�AC����ÿ��1����λ���ȵ��ٶ����C�������˶���ͬʱ������Q�ӵ�O���������߶�OB����ÿ��1����λ���ȵ��ٶ����B�������˶���������һ�㵽���յ�ʱ����һ����ֹ֮ͣ�˶������˶�ʱ��Ϊt�룮����PQ��
x2+bx+c��ͼ���������ύ��A��B��C���㣬���е�A������Ϊ����3��0������B������Ϊ��4��0��������AC��BC������P�ӵ�A���������߶�AC����ÿ��1����λ���ȵ��ٶ����C�������˶���ͬʱ������Q�ӵ�O���������߶�OB����ÿ��1����λ���ȵ��ٶ����B�������˶���������һ�㵽���յ�ʱ����һ����ֹ֮ͣ�˶������˶�ʱ��Ϊt�룮����PQ��
��1����գ�b�� ��c�� ��
��2���ڵ�P��Q�˶������У���APQ������ֱ������������˵�����ɣ�
��3����M���������ϣ��ҡ�AOM��������AOC�������ȣ������M�����ꡣ
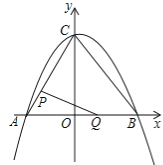
���𰸡���1��![]() ��4����2����������ֱ�������Σ�����������3��M(1,4)��M(
��4����2����������ֱ�������Σ�����������3��M(1,4)��M(![]() ,-4����M(
,-4����M(![]() ,-4��
,-4��
��������
(1)�������ߵĽ���ʽΪy=a��x+3����x-4������a=-![]() ����ɵõ������ߵĽ���ʽ���Ӷ���ȷ����b��c��ֵ��
����ɵõ������ߵĽ���ʽ���Ӷ���ȷ����b��c��ֵ��
��2������õ�C�����꣬���ݹ��ɶ��������AC=5����PC=5-t��AQ=3+t,���жϵ���APQ��ֱ��������ʱ�����APQ��90�����Ӷ��ó�![]() AOC
AOC![]() APQ���õ�����ʽ�з�����⼴�ɣ�
APQ���õ�����ʽ�з�����⼴�ɣ�
(3)���ݵ�M���������ϣ������M������Ϊ��m����![]() m2+
m2+![]() m+4�����ٸ�����AOM���������AOC�������ȣ��Ӷ��ó���
m+4�����ٸ�����AOM���������AOC�������ȣ��Ӷ��ó���![]() m2+
m2+![]() m+4=
m+4=![]() ���ⷽ�̼��ɣ�
���ⷽ�̼��ɣ�
�⣺��1���������ߵĽ���ʽΪy��a��x+3����x��4������a����![]() ����ã�y����
����ã�y����![]() x2+
x2+![]() x+4��
x+4��
��b��![]() ��c��4��
��c��4��
��2���ڵ�P��Q�˶������У���APQ��������ֱ�������Σ�
�������£����ڵ�P��Q�˶������У���PAQ����PQAʼ��Ϊ��ǣ�
�൱��APQ��ֱ��������ʱ�����APQ��90����
��x��0���������ߵĽ���ʽ�ã�y��4��
��C��0��4�����ߵ�A������Ϊ����3��0����
����Rt��AOC�У����ݹ��ɶ����ã�AC��5��
��AP��OQ��t����AQ=3+t��
�ߡ�OAC����PAQ����APQ����AOC
��![]() AOC
AOC![]() APQ
APQ
��AP:AO=AQ:AC
��![]() =
=![]() ��t=4.5��
��t=4.5��
���������֪��0��t��4��
��t��4.5�������⣬����APQ��������ֱ�������Σ�
(3 )���M��������m����![]() m2+
m2+![]() m+4��
m+4��
�ߡ�AOM���������AOC�������ȣ��ҵ�ΪAO��C��0��4����
�ੁ![]() m2+
m2+![]() m+4=
m+4=![]()
����![]() m2+
m2+![]() m+4=-4ʱ����ã�m=
m+4=-4ʱ����ã�m=![]() ��
��![]() ,
,
����![]() m2+
m2+![]() m+4=4ʱ����ã�m=1��0
m+4=4ʱ����ã�m=1��0
�ߵ�m=0ʱ����C�غϣ���m=![]() ��
��![]() ��1
��1
�� M(1,4)��M(![]() ,-4����M(
,-4����M(![]() ,-4��
,-4��


 ����С״Ԫ��������������ϵ�д�
����С״Ԫ��������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ1��������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ��
��![]() ��
��
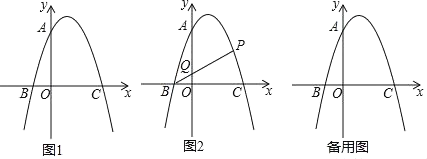
��1���������߽���ʽ��
��2����ͼ2����![]() �������ߵ�һ������һ�㣬����
�������ߵ�һ������һ�㣬����![]() ��
��![]() ���ڵ�
���ڵ�![]() �����
�����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ���߶�
���߶�![]() ��Ϊ
��Ϊ![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��3���ڣ�2���������£�����![]() ��ֱ��
��ֱ��![]() �ᣬ��
�ᣬ��![]() ��ȡһ��
��ȡһ��![]() ����
����![]() �ڵڶ����ޣ�������
�ڵڶ����ޣ�������![]() ��ʹ
��ʹ![]() ������
������![]() ���ӳ�
���ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��
��![]() ����
����![]() ʱ����
ʱ����![]() ֵ��
ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��AC��10��tanA��2��BE��AC�ڵ�E��D���߶�BE�ϵ�һ�����㣬��![]() ����Сֵ��( )
����Сֵ��( )
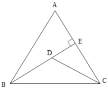
A. ![]() B.
B. ![]() C.
C. ![]() D. 10
D. 10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() �DZ߳�Ϊ
�DZ߳�Ϊ![]() �ĵȱ������Σ�����
�ĵȱ������Σ�����![]() ��
��![]() ͬʱ��
ͬʱ��![]() ��
��![]() ����������ֱ���
����������ֱ���![]() ��
��![]() �����˶������е�
�����˶������е�![]() �˶����ٶ���
�˶����ٶ���![]() ����
����![]() �˶����ٶ���
�˶����ٶ���![]() ������
������![]() �����
�����![]() ʱ��
ʱ��![]() ��
��![]() ���㶼ֹͣ�˶������˶�ʱ��Ϊ
���㶼ֹͣ�˶������˶�ʱ��Ϊ![]() ������������⣺
������������⣺
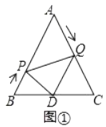
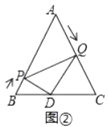
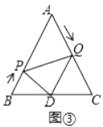
��1����ͼ�٣���![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��
��2����ͼ�ڣ���![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() Ϊֱ�������Σ�
Ϊֱ�������Σ�
��3����ͼ�ۣ���![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ����
����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��![]() ���ƣ�
���ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�������ABC�У�AD�ǡ�BAC��ƽ���ߣ�EΪAD��һ�㣬��BEΪһ������BE�·����ȱ�������BEF������CF��
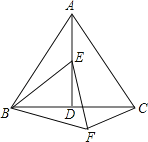
��1����֤����ABE�ա�CBF��
��2�����ACF�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����¹ڷ��ס���Ű����������Ӣ��ӿ�֣�������λ����Ӣ��������ɽ�������ꡢ���������Ŷ�����μ�ΪA��B��C��D����Ϊ��ͬѧ���˽���λ���¼�����ʦ������»��ȡ������ȫ��ͬ�Ŀ�Ƭ���ֱ�д��A��B��C��D�ĸ���ţ�Ȼ���泯�Ϸ��ã����Ⱥ�ÿ��ͬѧ���������ȡһ�ţ����±�ź�Żأ���ʦҪ��ÿλͬѧ���ݳ鵽�Ŀ�Ƭ�ϵı�Ų�����Ӧ����Ӣ�۵����ϣ�������С����

��1��������ֿ�Ƭ������鵽���ΪC�ĸ���Ϊ�� ����
��2��ƽƽ�Ͱ�����λͬѧ�鵽�Ŀ�Ƭ�Dz�ͬӢ�۵ĸ����Ƕ��٣�����״ͼ���б��ķ�����ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)�Ȼ�������ֵ��(a+b)(a��b)+(a+b)2-2a2������a=��2��![]() ��b=
��b=![]() ��2
��2
(2)��ͼ�٣�С�����̨�Ϸ�����һ�����۵���ɹ�¼ܣ�ͼ����ɹ�¼ܵIJ���ʾ��ͼ����������OC=OD=126cm��OA=OB=56cm����AB=32cm�����ʱC��D�����ľ��룮
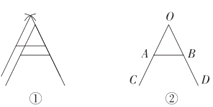
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���������ɼ�������������ļ۸�Ϊ![]() Ԫʱ��ÿ����ס�Ĺ�����Ϊ
Ԫʱ��ÿ����ס�Ĺ�����Ϊ![]() �䣬���г�����������ñ���ÿ������ļ۸���
�䣬���г�����������ñ���ÿ������ļ۸���![]() Ԫ֮�䣨��
Ԫ֮�䣨��![]() Ԫ��
Ԫ��![]() Ԫ������ʱ��ÿ����ס�ķ�����
Ԫ������ʱ��ÿ����ס�ķ�����![]() ���䣩��ÿ������ļ۸�
���䣩��ÿ������ļ۸�![]() ��Ԫ�����������±���
��Ԫ�����������±���
| ���� | 190 | 200 | 210 | 220 | ���� |
| ���� | 65 | 60 | 55 | 50 | ���� |
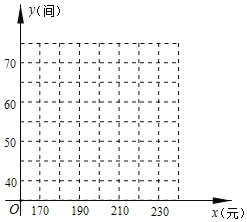
��1��������������������ϵ�������Ӧ�ĵ㣬������ͼ��
��2�����루1���е�ͼ����ʲô������ͼ����![]() ����
����![]() �ĺ�������ʽ����д���Ա���
�ĺ�������ʽ����д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����ͷ�����Ӫҵ��ΪW (Ԫ)�����������������أ��ʱ��ݱ����ļ۸�Ϊ����Ԫʱ���ͷ�����Ӫҵ��������Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ȫ��������ѧУ���뿪չ��һ����Ҫ������ijУΪ���˽�ҳ���ѧ�����������ڰ�ȫ֪ʶѧϰ������������������ϲ��ԣ����ڱ�Уѧ���������ȡ����ѧ�����е��飮���Ѳ�����Ե������Ϊ![]() �����Σ�
�����Σ�![]() ����ѧ���Լ����룻
����ѧ���Լ����룻![]() ���ҳ���ѧ��һ����룻
���ҳ���ѧ��һ����룻![]() �����ҳ��Լ����룻
�����ҳ��Լ����룻![]() ���ҳ���ѧ����δ���룮���ݵ�����������������²�������ͳ��ͼ�������ͼ���ṩ����Ϣ������������⣺
���ҳ���ѧ����δ���룮���ݵ�����������������²�������ͳ��ͼ�������ͼ���ṩ����Ϣ������������⣺
![]() ����γ��������У��������� ��ѧ����
����γ��������У��������� ��ѧ����
![]() ��ȫ����ͳ��ͼ������������ͳ��ͼ��
��ȫ����ͳ��ͼ������������ͳ��ͼ��![]() ������Ӧ���ε�Բ�ĽǵĶ�����
������Ӧ���ε�Բ�ĽǵĶ�����
![]() ���ݳ��������������Ƹ�У
���ݳ��������������Ƹ�У![]() ��ѧ�������ҳ���ѧ����δ��������������
��ѧ�������ҳ���ѧ����δ��������������
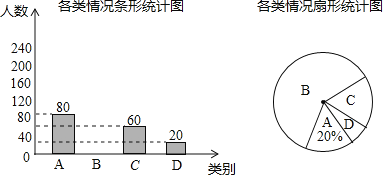
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com