试题分析:(1)由AB为⊙O的直角,根据圆周角定理得到∠ACB=90°,即∠1+∠3=90°,再根据切线的性质得OC⊥CG,则∠3+∠GCA=90°,然后利用等量代换即可得到∠1=∠GCA;
(2)由DE⊥AB得到∠AEF=90°,再根据等角的余角相等可得到∴∠AFE=∠ABC=m°,然后利用对顶角相等有∠DFC=∠AFE=m°;
(3)由∠GCA=∠1,∠DFC=∠ABC易得∠GCF=∠GFC,根据等腰三角形的判定得到GF=GC,由GD=GF得到GD=GC,则∠2=∠4,利用三角形内角和得∠2+∠GCF=
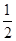
×180°=90°,即∠DCF=90°,而∠ACB=90°,于是得到点B、C、D共线,然后根据旋转的性质得到△ABC以AB为腰的等腰三角形,且顶角∠BAC=β,则根据三角形内角和定理易得β=180°-2∠ABC.
试题解析:(1)证明:如图:
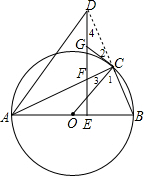
∵AB为⊙O的直角,
∴∠ACB=90°,即∠1+∠3=90°,
∵GC为⊙O的切线,
∴OC⊥CG,
∴∠OCG=90°,即∠3+∠GCA=90°,
∴∠1=∠GCA,
即∠GCA=∠OCB;
(2)∵∠ACB=90°,
∴∠ABC+∠BAC=90°,
∵DE⊥AB,
∴∠AEF=90°,
∴∠AFE+∠EAF=90°,
∴∠AFE=∠ABC=m°,
∴∠DFC=∠AFE=m°;
(3)∠β=180°-2∠ABC.理由如下:
∵∠GCA=∠1,∠DFC=∠ABC,
而∠1=∠ABC,
∴∠GCF=∠GFC,
∴GF=GC,
∵G为DF的中点,
∴GD=GF,
∴GD=GC,
∴∠2=∠4,
∴∠2+∠GCF= ×180°=90°,即∠DCF=90°,
而∠ACB=90°,
∴点B、C、D共线,
∵以点A为旋转中心,以∠β(0°<β<90°)为旋转角度将B旋转到点D,
∴AD=AB,∠BAD=β,
∴∠ABD=∠ADB,
∴β+2∠ABC=180°,
即β=180°-2∠ABC.
考点: 圆的综合题.

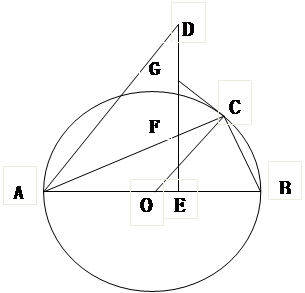
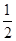 ×180°=90°,即∠DCF=90°,而∠ACB=90°,于是得到点B、C、D共线,然后根据旋转的性质得到△ABC以AB为腰的等腰三角形,且顶角∠BAC=β,则根据三角形内角和定理易得β=180°-2∠ABC.
×180°=90°,即∠DCF=90°,而∠ACB=90°,于是得到点B、C、D共线,然后根据旋转的性质得到△ABC以AB为腰的等腰三角形,且顶角∠BAC=β,则根据三角形内角和定理易得β=180°-2∠ABC.


